Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 17. 01. 2008 21:15 — Editoval martinko18 (17. 01. 2008 21:21)
- martinko18
- Zelenáč
- Příspěvky: 24
- Reputace: 0
Matematika 1
Caute, pomozte mi prosim s tymito prikladmi:
Link na lepsie zobrazenie zadania:
http://matematika.havrlant.net/forum/up … iklady.jpg
Viem, ze v Ulohe 2. je D(f)=R, ale neviem ako si to vysvetlit, ked diskriminant mi vysiel zaporny. Ci to zachranuje ta +1?
K 3. Ulohe by som sa este opytal, ci by sa nieco zmenilo vo vypocte keby tam namiesto cos bolo sin, alebo na co si treba davat pozor.
Ak sa da, napiste mi vysledky na tie priklady aj s postupom. Dakujem.
Offline
#2 17. 01. 2008 23:34
Re: Matematika 1
ad 1: resis nerovnici  , zaklady jsou stejne, takze resime
, zaklady jsou stejne, takze resime  , coz by nemel byt problem vyresit. spravny vysledek vzhuru nohama:
, coz by nemel byt problem vyresit. spravny vysledek vzhuru nohama:  .
.
ad 2: definicnim oborem logaritmu jsou kladna cisla, takze resime nerovnici  , kdyz si spocitas diskriminant, tak zjistis, ze vyjde zaporny, tudiz cela parabola je nad osou x -> definicni obor je cele R
, kdyz si spocitas diskriminant, tak zjistis, ze vyjde zaporny, tudiz cela parabola je nad osou x -> definicni obor je cele R
ad 3) ta absolutni hodnota muze nabyvat hodnot z intervalu 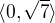 , takze celkove muze dana funkce nabyvat hodnot
, takze celkove muze dana funkce nabyvat hodnot 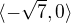 .
.
Offline
#3 17. 01. 2008 23:59
- martinko18
- Zelenáč
- Příspěvky: 24
- Reputace: 0
Re: Matematika 1
↑ plisna:
dakujem za pomoc (och, keby som to vedel tak dobre ako ty :) )
toto forum je fakt pecka :)
Offline