Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 04. 09. 2009 10:44 — Editoval Tlama (04. 09. 2009 10:45)
Konvergence řady
Dobrý den potřeboval bych poradit s konvergencí řady:.
Zkusil jsem použít limitní Raabeovo kritérium s výsledkem 0, tudíž by měla být řada divergentní, ale nemohu se shodnout s kolegy kteří tvrdí že tato řada je konvergentní. Děkuji za pomoc.
Offline
#2 04. 09. 2009 11:08
- kaja(z_hajovny)

- Místo: Lážov
- Příspěvky: 1002
- Reputace: 12
- Web
Re: Konvergence řady
zkuste sem napsat postup.
ale srovnani s 1/n^2 ukazuje, ze konverguje.
Offline
#7 04. 09. 2009 12:29 — Editoval LukasM (04. 09. 2009 13:00)
Re: Konvergence řady
↑ Tlama:
Aha, ok. Takže vyšetřuješ konvergenci mocninné řady v krajním bodě oboru konvergence, chápu to dobře?
Potom je ale nesmysl vracet se k tomu původnímu zadání. Počítáš prostě konvergenci té řady na jakou sis to upravil, a zadání původní tě nezajímá. Sice by to vyšlo asi taky, ale tím žes to upravil si máš ten výpočet zjednodušit, tedy určit to prostě z hlavy srovnáním s  .
.
V tom Raabeově kritériu máš jinak nejspíš špatně dosazené to x, ale upřímně jsem to moc nezkoumal (Edit: po lepším prozkoumání uznávám, že tohle je kec, dosazené je správně, špatně je jen výsledek). A ještě technická.. nemá být správný tvar po úpravě  ? Na charakteru řady to sice nic nemění, ale nějak teď rychle nevím proč je tam mínus.
? Na charakteru řady to sice nic nemění, ale nějak teď rychle nevím proč je tam mínus.
Offline
#8 04. 09. 2009 12:34
Re: Konvergence řady
↑ Tlama:
Tak řada 
evidentně konverguje, a dokázat se to dá triviálně, nejen porovnáním s notoricky známou řadou 1/n^2, ale i přímým odvozením, např. srovnáním s evidentně konvergentní řadou 1/[n*(n-1)].
BTW, jakže se dokáže, jaký je součet řady 1/n^2? :) Jak se dokáže, že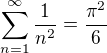
Já to v tomhle okamžiku sám nevím :)
Offline
#11 04. 09. 2009 12:57
Re: Konvergence řady
↑ Tlama:
Ok, tak že seš to ty, tak jsem to prošel. V tom cos napsal je dosazeno dobře, v tom jsem kecal, omlouvám se. Ale není pravda že to vyjde nula. Nezapomeň, že počítáš limitu toho výrazu. V čitateli a jmenovateli máš dohromady čtyři dvojky s nějakou mocninou, když je dáš dohromady, vyjde 2^0, tedy jednička. Spočítat limitu toho zbytku snad už nebude problém. Mně vyšla 2.
A když do toho Raabeho použiješ už tu upravenou řadu, odpadne ti to krácení dvojek a hodně psaní (de facto jsi to udělal při té úpravě). Výsledek bude stejný. Ale jak píšu já i ostatní, proč do toho tahat Raabeho, když je po té úpravě přímo vidět, že to konverguje..
Je to jasné?
Offline
#12 04. 09. 2009 13:03
Re: Konvergence řady
↑ Mephisto:
Možná bych kolegu zbytečně nezatěžoval těmito důkazy, postačí si pamatovat, že  konverguje právě když
konverguje právě když  . To pro řešení příkladů myslím stačí.
. To pro řešení příkladů myslím stačí.
Offline
#14 07. 09. 2009 09:27 — Editoval Rumburak (22. 10. 2013 17:39)
Re: Konvergence řady
↑ Mephisto:
Řadu 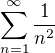 lze sečíst pomocí Fourierových řad - V.Jarník v Integrálním počtu 2
lze sečíst pomocí Fourierových řad - V.Jarník v Integrálním počtu 2
(kapitoly Fouierovy řady, Orthogonální systémy) uvádí dva způsoby.
Pokusím se zde popsat další způsob, který využívá některých zajímavých triků s integrály.
Označme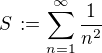 ,
, 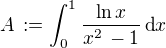 ,
, 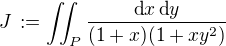 , kde
, kde 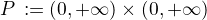 .
.
Lemma 1. 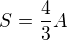 .
.
Lemma 2.
 .
.Lemma 3.
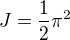 .
.Celkem tedy
 .
. Offline



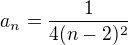 ,
, 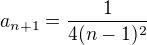 Kde jsi přišel k tomu 2^(-n)?
Kde jsi přišel k tomu 2^(-n)?


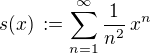 pro
pro ![kopírovat do textarea $x\in [-1,\,1]$](/mathtex/6f/6f095dc94622b97a2c9d4bdef7e4d1b3.gif) , kde tato mocninná řada konverguje. Uvnitř tohoto intervalu je
, kde tato mocninná řada konverguje. Uvnitř tohoto intervalu je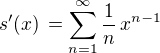 ,
, 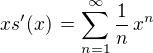 ,
, 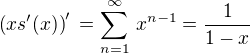 ,
, 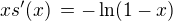 ,
, 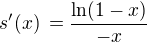 (v posledním vzorci předpokládáme též
(v posledním vzorci předpokládáme též  ).
).  v bodě 1 zleva (Abelova věta) plyne
v bodě 1 zleva (Abelova věta) plyne 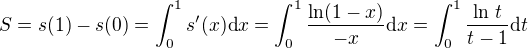 .
.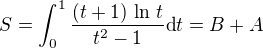 , kde
, kde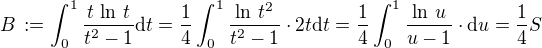 dle výsledku (1).
dle výsledku (1).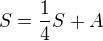 , tedy
, tedy 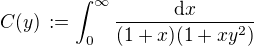 pro
pro  . Je-li navíc
. Je-li navíc 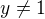 , obdržíme
, obdržíme ![kopírovat do textarea $C(y) \,= \int_0^\infty \(\frac{1}{1-y^2}\cdot\frac{1}{1+x}\,-\,\frac{y^2}{1-y^2}\cdot\frac{1}{1+xy^2}\)\text{d}x \,=\, \frac{1}{1-y^2}\cdot \[\ln (1+x) -\ln (1+xy^2) \]_{x=0}^\infty = $](/mathtex/94/944e6ae39019d007d8fd85f1f25d0372.gif)
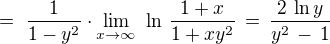 .
.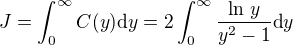 .
. ,
,  , jak zjistíme substitucí
, jak zjistíme substitucí 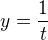 .
. .
.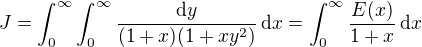 , kde
, kde ![kopírovat do textarea $E(x) \,:=\int_0^{\infty}\frac{\text{d}y}{1+xy^2}= \[\frac{1}{\sqrt{x}}\,\text{arctg}\, (\sqrt{x}y)\]_{y=0}^{\infty}= \frac{\pi}{2\sqrt{x}}$](/mathtex/11/1118bbb90b4912baf0b017dde800cf06.gif) ,
,![kopírovat do textarea $J=\,\pi\int_0^{\infty}\frac{1}{1+x}\cdot\frac{\text{d}x}{2\sqrt{x}}= \pi [\text{arctg} \,\sqrt{x}]_{0}^{\infty}=\frac{1}{2}\pi^2$](/mathtex/69/69eaab4941ef4b5b8100947df0563fb3.gif) .
.