Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 02. 03. 2009 19:31
Re: Diofantická rovnice
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#4 16. 05. 2009 14:08
#5 15. 09. 2009 23:09
- check_drummer

- Příspěvky: 5446
- Reputace: 106
Re: Diofantická rovnice
Bez výpočtu:
"Máte úhel beta." "No to nemám."
Offline
#6 15. 09. 2009 23:46
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Diofantická rovnice
Offline
#7 17. 09. 2009 00:36
- check_drummer

- Příspěvky: 5446
- Reputace: 106
Re: Diofantická rovnice
"Máte úhel beta." "No to nemám."
Offline
#8 17. 09. 2009 01:31
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Diofantická rovnice
Offline
#9 17. 09. 2009 22:45
- check_drummer

- Příspěvky: 5446
- Reputace: 106
Re: Diofantická rovnice
"Máte úhel beta." "No to nemám."
Offline
#10 17. 09. 2009 23:41
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Diofantická rovnice
Offline
#11 18. 09. 2009 00:01
- check_drummer

- Příspěvky: 5446
- Reputace: 106
Re: Diofantická rovnice
↑ BrozekP:
Přesně tak, jako zlatokopové na Clondyke. :-)
"Máte úhel beta." "No to nemám."
Offline
 .
.![kopírovat do textarea $ [x(x+3)][(x+1)(x+2)]=y^2\nl (x^2+3x)(x^2+3x+2)=y^2\nl \text{subst. }z:=x^2+3x\nl z(z+2)=y^2\nl z^2+2z=y^2\nl z^2+2z+1=y^2+1\nl (z+1)^2=y^2+1\nl \text{subst. }u:=z+1\nl u^2-y^2=1\nl (u-y)(u+y)=1 $](/mathtex/c7/c731d3b29271dba522635ae2e6e37196.gif)
 a
a  , pak
, pak  , nebo
, nebo  a
a  , pak
, pak  .
. . Pak
. Pak 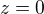 a
a  . První dvě řešení jsou tedy
. První dvě řešení jsou tedy
 . Pak
. Pak  a
a  . Další dvě řešení jsou tedy
. Další dvě řešení jsou tedy
 . Ovšem na pravé straně rovnice je čtverec, který ovšem musí obsahovat činitel tvaru
. Ovšem na pravé straně rovnice je čtverec, který ovšem musí obsahovat činitel tvaru  (eventuelně pro k = 0). To pro žádná k a n není možné splnit, tedy pro x >=1 řešení neexistuje. Stejnou úvahou pro záporná čísla dospějeme k tomu, že pro x <= - 4 rověž řešení neexistuje. Tedy zbývá případ nuly a ta se na levé straně nabyde pro x = -3, -2, -1, 0 a na pravé pro y = 0, tedy řešením jsou tyto 4 dvojice x,y.
(eventuelně pro k = 0). To pro žádná k a n není možné splnit, tedy pro x >=1 řešení neexistuje. Stejnou úvahou pro záporná čísla dospějeme k tomu, že pro x <= - 4 rověž řešení neexistuje. Tedy zbývá případ nuly a ta se na levé straně nabyde pro x = -3, -2, -1, 0 a na pravé pro y = 0, tedy řešením jsou tyto 4 dvojice x,y. . Levá strana tedy obsahuje sudou mocninu dvojky.
. Levá strana tedy obsahuje sudou mocninu dvojky. . Což ovšem není v přirozených číslech řešitelné (jediná nabízející se možnost m = n+1 ji neřeší). Tedy buď je jedno z čísel dělitelné 6 nebo je jedno dělitelné 9 a není dělitelné 2. Ovšem druhá možnost nemůže nastat, protože pak by toto číslo mělo vlastnost A a opět dostaneme neřešitelnou rovnici. Tedy z toho plyne, že x a x+3 jsou dělitelné 3 a jedno ze 4 čísel (x až x+3) je dělitelné 6 a druhé je dělitelné lichou mocninou 3 (platnost dělitelnosti 2 a 4 je stále samozřejmě splněna).
. Což ovšem není v přirozených číslech řešitelné (jediná nabízející se možnost m = n+1 ji neřeší). Tedy buď je jedno z čísel dělitelné 6 nebo je jedno dělitelné 9 a není dělitelné 2. Ovšem druhá možnost nemůže nastat, protože pak by toto číslo mělo vlastnost A a opět dostaneme neřešitelnou rovnici. Tedy z toho plyne, že x a x+3 jsou dělitelné 3 a jedno ze 4 čísel (x až x+3) je dělitelné 6 a druhé je dělitelné lichou mocninou 3 (platnost dělitelnosti 2 a 4 je stále samozřejmě splněna). - jedno je dělitelné dvěma a ne čtyřmi (2), ale druhé (4) je sice dělitelné 4, ale ne lichou mocninou dvojky větší než dva.
- jedno je dělitelné dvěma a ne čtyřmi (2), ale druhé (4) je sice dělitelné 4, ale ne lichou mocninou dvojky větší než dva. . Nyní vytěžím aspoň jeden plod z mých předchozích úvah - totiž ten, že neexistují dvě přirozená (a analogicky ani dvě záporná) čísla, jejichž rozdíl je 2 a jejichž součin dá čtverec (to je bod (*)) a tedy ani náš upravený výraz nemůže být čtverec. Tj. jak jsem uvedl dříve - jediná řešení jsou pro y=0 a příslušné hodnoty x "motající se kolem 0".
. Nyní vytěžím aspoň jeden plod z mých předchozích úvah - totiž ten, že neexistují dvě přirozená (a analogicky ani dvě záporná) čísla, jejichž rozdíl je 2 a jejichž součin dá čtverec (to je bod (*)) a tedy ani náš upravený výraz nemůže být čtverec. Tj. jak jsem uvedl dříve - jediná řešení jsou pro y=0 a příslušné hodnoty x "motající se kolem 0".