Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z algebry
- » Blízkost mocnin prvočísel (TOTO TÉMA JE VYŘEŠENÉ)
#1 24. 09. 2009 23:02
- check_drummer

- Příspěvky: 4952
- Reputace: 106
Blízkost mocnin prvočísel
Ahoj,
platí následující hypotéza? Pro libovolná prvočísla p a q existují přirozená čísla k a n tak, že:  a pokud ano, existuje takových k a n nekonečně mnoho?
a pokud ano, existuje takových k a n nekonečně mnoho?
Pokud věta neplatí, existuje nějaký protipříklad?
Díky
"Máte úhel beta." "No to nemám."
Offline
#2 25. 09. 2009 00:15
Re: Blízkost mocnin prvočísel
Trocha úvah:
Ten rozdíl bude nulový pouze tehdy, když bude p=q (to je jasné). Dále bude moct nabývat jedničky pouze tehdy, když bude jedno z prvočísel dvojka. Pokud se bude jednat o dvě různá lichá prvočísla, pak jejich rozdíl (i jejich mocnin) nemůže být menší než 2.
Budeme-li mít 2 prvočísla ve tvaru 6k+1, pak jejich rozdíl (i jejich mocnin) bude nejméně 6, protože umocněním opět vznikne číslo ve tvaru 6k+1. To je protipříklad. Konkrétní takovou dvojicí může být třeba 7 a 13.
Offline
#3 25. 09. 2009 00:53
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Blízkost mocnin prvočísel
Nechť p=2 a q=3. Zřejmě 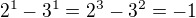 a
a  . Snadno ověříme, že toto jsou pro malá
. Snadno ověříme, že toto jsou pro malá  jediná vyhovující
jediná vyhovující  . Pro vyšší k je
. Pro vyšší k je  a proto
a proto  . Snadno ověříme, že možnost nepřichází v úvahu ani pro lichá ani pro sudá n, druhá možnost projde pouze pro sudá. Naopak uvážením mod 9 dostáváme, že k=3t. Řešíme proto
. Snadno ověříme, že možnost nepřichází v úvahu ani pro lichá ani pro sudá n, druhá možnost projde pouze pro sudá. Naopak uvážením mod 9 dostáváme, že k=3t. Řešíme proto  . Nejsem si jistý, jestli je to správná cesta, ale myslím, že jsem někde viděl důkaz, že pro větší k už žádné n nenajdeme, takže check_drummerova hypotéza neplatí.
. Nejsem si jistý, jestli je to správná cesta, ale myslím, že jsem někde viděl důkaz, že pro větší k už žádné n nenajdeme, takže check_drummerova hypotéza neplatí.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#4 25. 09. 2009 22:21
- check_drummer

- Příspěvky: 4952
- Reputace: 106
Re: Blízkost mocnin prvočísel
Díky za nápady. A co kdybychom dvojku na pravé straně poněkud pozměnili, např. zkoumaný výraz by měl tvar (při zachování ostatních uvedených podmínek):
kde úkolem je najít co nejmenší dvojici (d,c) reálných čísel - uspořádání dvojic uvažujeme lexikograficé - aby pro všechna p,q (spolu s platností ostatních podmínek úlohy) platila uvedená nerovnost (resp. uvést množinu dvojic (d,c), pro které nerovnost platí), případně ukázat, že žádná taková (d,c) neexistují.
"Máte úhel beta." "No to nemám."
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z algebry
- » Blízkost mocnin prvočísel (TOTO TÉMA JE VYŘEŠENÉ)