Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 25. 09. 2009 19:14 — Editoval beliqar (26. 09. 2009 10:29)
LA pro IT
zdravím,, vůbec nevím , neměl jsem na střední komplexní čísla nejspíš zabrždění učitelé aspon teda myslím že to je ono,,, mám vypočítat tretí odmocninu ze z
chtěl bych spíše pomoct s postupem,, myslím že musím vypočítat 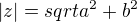 potom
potom 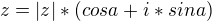
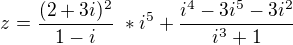 - vysledek vyjádřit v algebraickém tvaru
- vysledek vyjádřit v algebraickém tvaru
popř doporučit nějakou knihu či scripta či něco takového , kde jsou i matice atd.. protože mám tady i
Najděte spektrální rozklad matice
-1 -1 -1
-1 -2 0
-1 0 -2
díky moc
Offline
#2 25. 09. 2009 20:06 — Editoval Kondr (25. 09. 2009 20:33)
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: LA pro IT
Základy LA zde: ftp://math.feld.cvut.cz/pub/olsak/linal/linal.pdf
Spektrální rozklad tu: http://vondrak.am.vsb.cz/LA-IT/Practices/lacv14.pdf
K těm komplexním číslům: jak s nimi pracovat se dočteš tady http://cs.wikipedia.org/wiki/Komplexní číslo, tak zkus aspoň to číslo převést do algebraického tvaru. Odmocninu ze  pak spočítáš z Moivreovy věty.
pak spočítáš z Moivreovy věty.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#5 25. 09. 2009 20:34
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: LA pro IT
↑ beliqar:Promiň, asi jsem přehlédl slovo "třetí". Jak jsi to uvedl je to správně: převede se to do goniometrického tvaru, v něm se to odmocní a pak se to převede zpět. Vyjdou opravdu 3 výsledky.
↑ beliqar:i za nic nahradit nemůžeš, pouze využij rovnost  . Samotné i je něco jako
. Samotné i je něco jako  , ikdyž tento zápis není přesný.
, ikdyž tento zápis není přesný.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#6 25. 09. 2009 20:57 — Editoval beliqar (26. 09. 2009 10:30)
Re: LA pro IT
↑ Kondr:
no a to by mělo pokračovat nějak né ? 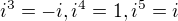 mám pravdu nebo né? jsem mimo školu rok a pul tak mi to moc nejde
mám pravdu nebo né? jsem mimo školu rok a pul tak mi to moc nejde
je ta úprava dobře ?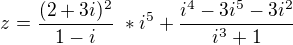
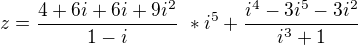
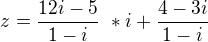
a ted nevím přesně ,,,
mám pokračovat takhle ? 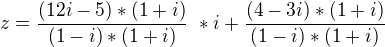
jeslti jo tak potom 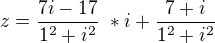
a tohle mám udělat ?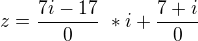 nebo to mám tak nechat ? ale když se to dělí nulou tak to potom nejde né ?
nebo to mám tak nechat ? ale když se to dělí nulou tak to potom nejde né ?
kdyby tě to náhodou rozesmálo, tak se nebudu divit :) já nemohl vypočítat normální ty komplexní čísla když jsem to viděl poprvé tak cca týden zpět a oni mi dají takový projekt už :)
Offline
#8 25. 09. 2009 22:01
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: LA pro IT
↑ beliqar: v jmenovateli nebude nula po usměrnění, ale 2, jelikož platí užitečný vzorec 2.1
Offline
#9 25. 09. 2009 22:09 — Editoval beliqar (25. 09. 2009 22:23)
Re: LA pro IT
↑ jelena:
díky díky,, ale jenom mi stručně řekni proč :))) abych věděl proč to dělám
takže podle toho bych měl 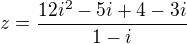
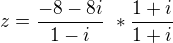
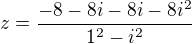
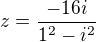
myslíš takhle ? a ten spodek udělám takhle nebo to nechám ? 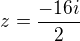
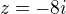 <<<<tohle je z ??? takže to je
<<<<tohle je z ??? takže to je 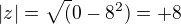 <<<takže tohle je abs z ? oprava -- jsem uplně zmatený dneska
<<<takže tohle je abs z ? oprava -- jsem uplně zmatený dneska
Offline
#10 25. 09. 2009 22:19 — Editoval jelena (25. 09. 2009 22:25)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: LA pro IT
↑ beliqar: stručně - co proč? Protože je to menší počet operací, vedoucí ke se stejnému výsledku, jako tvoje úprava - což by budoucího IT mělo zajimat nejvíce. Nebo jiné "proč"?
v 2. řádku se má ze stejného důvodu vytknout (-8), ale to je detail. Výsledek pro z=-8i je v pořádku (snad). Absolutní hodnota nemůže být záporné číslo.
Výsledek je v pořádku, děkuji informatikum :-)
Offline
#11 25. 09. 2009 22:24 — Editoval beliqar (25. 09. 2009 22:25)
Re: LA pro IT
↑ jelena:
jojo jasně,, já jsem z matiky měl vždycky dobré známky a všechno jsem chápal,, ale jsem mimo školu cca rok a půl a měl jsem jiné starosti -- tak se snažím dostat do starých kolejí,, přece jenom když to nepoužíváš tak to zapomeneš že ano,, ale každou chybou co mě opravujete si znova obnovuju znalosti a za to díky ..
Offline
#12 25. 09. 2009 22:28
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: LA pro IT
↑ beliqar: Ano, ano - však se snažíme, zdravím kolegu Kondra :-)
(přidala jsem edit do svého příspěvku - strojové ověření) Tak pokračuj, ať se vede.
Offline
#14 25. 09. 2009 22:41 — Editoval Kondr (25. 09. 2009 22:42)
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: LA pro IT
↑ beliqar:Zapoměl jsi odmocnit tu absolutní hodnotu. Navíc argument je  a ne
a ne  , takže výsledky jsou
, takže výsledky jsou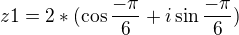
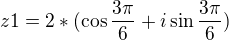
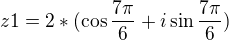
(nevím, co byl překlep a co výpočetní chyba, tak to nebudu hlouběji komentovat, kdyžtak se zeptej. Každopádně i má být u sinu.)
↑ jelena:Taky zdravím :o)
---
Kongo kanady a khaki kabát, dobytčák trambus a už chci padat, za zády chci nechat město svý, no to se ví!
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#17 25. 09. 2009 23:30
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: LA pro IT
↑ beliqar:To sice jo, ale ![kopírovat do textarea $|\sqrt[3]{z}|=\sqrt[3]{|z|}=\sqrt[3]{8}=2$](/mathtex/27/27c7fd9746ef265bc67a4ba9b7c69731.gif) . Jinak
. Jinak 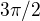 a
a  jsou dva způsoby vyjádření téhož. Pro
jsou dva způsoby vyjádření téhož. Pro 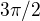 je pak argument třetí odmocniny
je pak argument třetí odmocniny 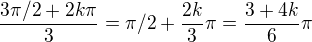 . Kontrola: mezi výsledky musí být 2i.
. Kontrola: mezi výsledky musí být 2i.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#18 25. 09. 2009 23:37 — Editoval beliqar (26. 09. 2009 00:11)
Re: LA pro IT
↑ Kondr:
jo jasně to vypočítám a pak jsem to zapomněl udělat v tom z1-3 ,, já myslel že to mám udělat přímo tu třetí jak jsem počítal |z|
jo takhle takže když budu mít 4odmocninu tak budu mít zase ![kopírovat do textarea $|\sqrt[4]{z}|=\sqrt[4]{|z|}=\sqrt[4]{8}=1,6...:) $](/mathtex/d9/d990470a98f586a103abcb2d6d9edb82.gif) popř...
popř... ![kopírovat do textarea $|\sqrt[n]{z}|=\sqrt[n]{|z|}=\sqrt[n]{z}=x$](/mathtex/6c/6c42e5fbd27a704781660c3d5045f20b.gif) ,,, takže opraví tu dvojku a mám to,,, viz výše a řekni pls jestli ok konečně :) už jsem z toho nanervy :))
,,, takže opraví tu dvojku a mám to,,, viz výše a řekni pls jestli ok konečně :) už jsem z toho nanervy :))
btw 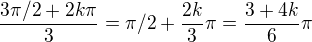
to  se bere 0,1,2..n ?
se bere 0,1,2..n ?
akorát tu kontrolu co si napsal moc nechápu to 2i
Offline
#19 26. 09. 2009 00:06
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: LA pro IT
1) S tou absolutní hodnotou -- v principu to asi chápeš, akorát ![kopírovat do textarea $\sqrt[4]{8}=1.681...$](/mathtex/0a/0add4e4ede3a4d260ef4e83c7534b024.gif)
2) to k se bere 0,1,2 (pro n-tou odmocninu 0,1,...,n-1). Mohlo by se brát i vyšší, ale pak by vycházela znovu ta stejná čísla.
3) s tou kontrolou jsem to myslel tak, že lehce ověříme, že 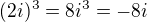 . Proto po převedení do algebraického tvaru musí jeden z výsledků být 2i.
. Proto po převedení do algebraického tvaru musí jeden z výsledků být 2i.
Už je to jasné?
---
Vždyť já jsem volnej jako pták, jezdím jen tak pod širák, s kompasem a s buzolou, hvězdy nad hlavou mi žhnou.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#20 26. 09. 2009 00:15 — Editoval beliqar (26. 09. 2009 00:27)
Re: LA pro IT
↑ Kondr:
Takže konečně správný výsledek by měl být tenhle .... ještě si to přečtu celé atd... popř. mi řekni jestli to je správně ale podle ověření co jsi psal určitě (btw jak to ověřím ještě na ty ostatní ? to asi ověřím jedině když mi výjde "z" určíté číslo že ? např těch 8,,, popř kdyby byla 4 a byla to druhá odmocnina, tak jeden z výsledku by byl 2 ??? )) a celkem to chápu na to že jsem to bral cca 2h :))) a mnohokrát díky za ochotu a tvůj čas :)![kopírovat do textarea $ z1= \sqrt[3]8*( \text {cos} \frac {\pi}{2}\ +i*\text {sin} \frac {\pi}{2})\ $](/mathtex/11/11115dc582d06140d4746fcc5d44a86c.gif) >>>>>
>>>>> 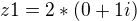 >>>>>
>>>>> 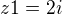
![kopírovat do textarea $ z2= \sqrt[3]8*( \text {cos} \frac {7\pi}{6}\ +i*\text {sin} \frac {7\pi}{6})\ $](/mathtex/1e/1e01bcf7ee956a551bb354551042882b.gif) >>>>>
>>>>> 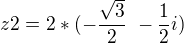 >>>>>
>>>>> 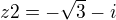
![kopírovat do textarea $ z3= \sqrt[3]8*( \text {cos} \frac {11\pi}{6}\ +i*\text {sin} \frac {11\pi}{6})\ $](/mathtex/a5/a554b28db6b617c92c79e2cd2660c8ef.gif) >>>>>
>>>>> 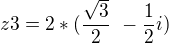 >>>>>
>>>>> 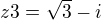
Offline
#21 26. 09. 2009 00:25
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: LA pro IT
↑ beliqar:Jo, to potvrdí i stroj. Rád jsem pomohl a musím podotknout, že tato diskuse vedla k výsledku hlavně díky Jeleně (já jsem čím dál línější upravovat takovéhle výrazy).
----
Jenom chleba kus a huspeninu, jako Robinson na pevninu, Tak já pospíchám hledat dětství svý. No to se ví!
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#22 26. 09. 2009 00:28 — Editoval beliqar (26. 09. 2009 00:42)
Re: LA pro IT
↑ Kondr:
jj to ti věřím,, jenom jak to vidíš ty základní chyby tak se musíš u pc převracet :)
později budu pokračovat s tou matici :) podívám se na ty linky co si mi poslal popř. kdybych si nevěděl rady napíšu sem :) u jiné už jsem počítal převod do LU a prostě nevycházelo mi to ,, točil jsem se stále dokola..
0 2 1 1 0 0 ____ 0 2 1 1 0 0 ____
1 1 0 0 1 0 ____ 1 1 0 0 1 0_____
2 1 3 0 0 1 +(-2)r2::::: 0 -1 3 0 -2 1 ____
ted jsem se dočetl že to můžu přehazovat sloupce takže to zkiusím ,, a další ,,měl jsem si místo ř1 radš dát ř2 nebo tady když mám 0první a dávám to do LU nevadí? nebo to je stejné a měl bych si převést a11 na nenulovou že ? :))
Offline
#23 26. 09. 2009 00:45 — Editoval jelena (26. 09. 2009 08:59)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: LA pro IT
↑ beliqar:
Ten projekt snad máte na celý semestr, ne? Nech to alespoň na zítřek - zatím si čti.
↑ Kondr: děkuji, ale také už mi ubývá síl... Máme tedy vyřešeno 1/2 z 60- úplně dole na strance v LA pro IT.
"Ostatní se bez toho musejí obejit, protože tenhle šotek chce, abych se s ním vydala na cestu do světa, sama jako pouštní vítr nebo pěnkava."
"Ne, ne, ne! zvolal jsem se snadno pochopitelným znepokojením. "tak jsem to vůběc nemyslel!"
"Tak tedy jako mořský orel."
Offline
#24 26. 09. 2009 01:38
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: LA pro IT
↑ beliqar:Jak píšou na Wiki: An invertible matrix admits an LU factorization if and only if all its leading principal minors are non-zero. A to zde splněno není, už první minor je nula.
---
OT: doufám, že odkaz na zadání (zejména pátý příklad v DU) tu nenajde Halogan nebo jiný z typograficky citlivějších kolegů. :)
BRKOS - matematický korespondenční seminář pro střední školy
Offline
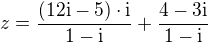
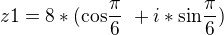
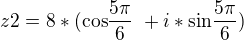
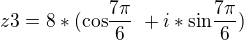
![kopírovat do textarea $ |\sqrt[3]z|= \sqrt[3] (0-8^2)= \sqrt[3]64 = 4 $](/mathtex/49/495ae4c4a0d1e6c240fc5fd766606234.gif)