Matematické Fórum

↑ Ivana:

1) Zapomněla jste zlogaritmovat tisícovku (i když v dalším kroku je zlogaritmovaná).
2) log x^2 není to samé jako [text]log^2 x[/tex].
3) není vhodné používat 'x' jako substituci za log x. Vaše a jsou ve skutečnosti a 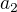, které zastupují . Po dosazení vychází a .

Už jen z Df logaritmu je jasné, že by zaporné číslo ve vašem výpoču nebylo možné použít.

Jen do ní! Chudák Ivana ten příklad vypočítá a vy jen hledáte chyby, že se nestydíte. Opravovat dokáže každej středoškolskej blbeček. :=))

Pro budoucí generace: V době psaní této zprávy měl halogan podpis, ve kterém se vyskytovalo slovní spojení „středoškolský blbeček“. Proto tato Gincova reakce. — Admin —

Mimochodem, ono hodit sem rovnici a ani nenapsat začátek, jak jsem to zkousel řešit a jak daleko jsem se dostal ..... To obdivuju Ivanu, že se vůbec pustila do odpovídání. Navíc to už asi není aktuální dotaz. Ale chápu že někdo by tenhle příklad mohl vyhrabat a mohlo by ho to mást.

↑ Ginco:

Tak to pardon. Já nechtěl znít nijak pejorativně nebo nepříjemně. Sám mám veliké problémy se spoustou věcí v matematice, takže sice rád pomůžu, ale taky si nechám rád poradit :) Takže můj první výstup zde nebyl naprosto úspěšný. Čas uzamknout toto téma, příklad je vyřešen.