Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 26. 09. 2009 13:46
Vektor
Částice vyletí z počátku soustavy souřadnic s počáteční rychlostí  pohybuje se s konstantním zrychlením
pohybuje se s konstantním zrychlením 
a) Jaká je její rychlost v okamžiku, kdy její x-ová souřadnice nabývá největší hodnoty?
b) Jaká je v tomto okamžiku její poloha?
Nějakou představu mám (předpokládám, že za a) je rychlost v=0 m.s-1) , ale potřeboval bych trochu nakopnout, jak to dokázat. Dík.
Offline
#2 26. 09. 2009 19:55
Re: Vektor
Zdravím,
a.) Správne :). Keďže zpočiatku sa teleso pohybuje v kladnom smere osy x a má zrýchlenie opačného smeru, jeho x-ová súradnica bude mať maximálnu hodnotu keď to "zrýchlenie zbrzdí počiatočnú rýchlosť".
b.) X-ovú súradnicu zrátame z X=1/2 . a.t^2 (bodobne to platí aj pre Y, ale musíme tam zobrať y-ovú hodmotu tohoto zrýchlenia) a v=a.t (aj tu muusíme zobrať x-ovú, alebo y-ovú hodnotu zrýchlenia a rýchlosti.).
Stačí tak?
You know who
(or maybe not)
Offline
#4 27. 09. 2009 20:03
Re: Vektor
Phill napsal(a):
Částice vyletí z počátku soustavy souřadnic s počáteční rychlostí
pohybuje se s konstantním zrychlením
a) Jaká je její rychlost v okamžiku, kdy její x-ová souřadnice nabývá největší hodnoty?
b) Jaká je v tomto okamžiku její poloha?
Nějakou představu mám (předpokládám, že za a) je rychlost v=0 m.s-1) , ale potřeboval bych trochu nakopnout, jak to dokázat. Dík.
Vyšlo mi a) 
b) 
Budu rád když na to někdo hodí voko, použil sem rovnice pro rovnoměrně zrychlený pohyb.
Dík.
Offline
#5 27. 09. 2009 21:54 — Editoval matoxy (27. 09. 2009 21:55)
Re: Vektor
a.) x-ovú zlošku si správne určil, že je nula, ale tá y-ová je nie dobre.
Ja by som rátal takto: Táto  rovnica nám hovorí, že x-ová zložka rýchlosti sa každú sekundu zmení (keďže počiatočná rýchlosť je opačného smeru ako zrýchlenie, bude spočiatku teleso spomaľovať) o 1 m.s^-1. Z rýchlosti 3 m.s^-1 spomalí za koľko?
rovnica nám hovorí, že x-ová zložka rýchlosti sa každú sekundu zmení (keďže počiatočná rýchlosť je opačného smeru ako zrýchlenie, bude spočiatku teleso spomaľovať) o 1 m.s^-1. Z rýchlosti 3 m.s^-1 spomalí za koľko?
Ten istý čas čo bude v x-ovom smere spomaľovať na nulu bude v y-ovom zrýchlovať z nuly na nejakú rýchlosť. So zrýchlením 0,5 za čas t zrýchli na 0,5t.
b.) Keď budeme mať čas za ktorý príde do tohoto bodu len to dosadíme do rovnice  , kde a je zrýchlenie, v_0 je počiatočná rýchlosť a s_0 je počiatočná dráha (v našom príklade je aj pre x aj pre y nulová)
, kde a je zrýchlenie, v_0 je počiatočná rýchlosť a s_0 je počiatočná dráha (v našom príklade je aj pre x aj pre y nulová)
Inak je dosť nezvyklé označovať smerový vektor 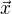 pretože písmenko x sa zaužívalo pre jednu z osí.
pretože písmenko x sa zaužívalo pre jednu z osí.
Ak je niečo nejasné, tak sa spýtaj:)
You know who
(or maybe not)
Offline


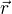 by bylo asi vhodnější
by bylo asi vhodnější