Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé středoškolské úlohy
- » Omezení sumy čísel -> omezení jejich maxima (TOTO TÉMA JE VYŘEŠENÉ)
#1 30. 09. 2009 22:10
- check_drummer

- Příspěvky: 4650
- Reputace: 101
Omezení sumy čísel -> omezení jejich maxima
Ahoj,
pro n > 3 dokažte:
platí-li  a
a  , potom
, potom 
"Máte úhel beta." "No to nemám."
Offline
#3 01. 10. 2009 16:16 — Editoval Rumburak (02. 10. 2009 09:13)
Re: Omezení sumy čísel -> omezení jejich maxima
↑ musixx:
Zdravím. Tvá úvaha je správná za předpokladu, že vždy bude  , to ale v zadání není řečeno,
, to ale v zadání není řečeno,
místo toho je tam předpoklad  , který má říci, že budou existovat
, který má říci, že budou existovat  , mající v tomto součtu
, mající v tomto součtu
"dosti velkou váhu".
Tím ale nechci naznačovat, že bych tuto úlohu měl vyřešenou :-) .
Protipříklad dokazující, že předpokládat pouze druhou nerovnost nestačí:  ,
, 
a není těžké najít i nějaký mnohem lepší.
Offline
#4 01. 10. 2009 22:08
- check_drummer

- Příspěvky: 4650
- Reputace: 101
Re: Omezení sumy čísel -> omezení jejich maxima
Je to tak, pro kladná čísla by bylo samozřejmě řešení triviální.
Dnes jsem o tom venku při dešti a větru lehce přemýšlel:
Je zřejmé (z druhé podmínky), že  , tj. buď max(ai) <= -2 nebo max(ai) >= 2.
, tj. buď max(ai) <= -2 nebo max(ai) >= 2.
Pro případ, kdy n=4 (nejmenší možné n), pokud by nastalo, že max(ai) <= -2 a (pro spor) ai < 2 pro všechna i, pak součet ai (díky tomu, že jsou jen 4) bude menší než 4 a tedy nebude splněna první podmínka.
K případu n > 4 jsem se zatím díky počasí nedostal, ale díky druhé podmínce se intuitivně jeví, že věta bude platit "tím spíše" (díky kvadrátu n na jedné straně, ale sčítáme jen n kvadrátů). Intuice samozřejmě nic neříká. Vidím dvě cesty - buď podobný důkaz sporem jako výše pro n=4 (se složitějšími možnostmi) a nebo indukci.
Takže to vidím pro tuto chvíli jako konec prvního dílu. :-)
"Máte úhel beta." "No to nemám."
Offline
#5 02. 10. 2009 13:58 — Editoval Marian (02. 10. 2009 14:32)
Re: Omezení sumy čísel -> omezení jejich maxima
PS.
Jenže to jsme dokázat nechtěli. Na chybu mě upozornil kolega musixx. Zkusím se zamyslet ještě později.
Offline
#6 02. 10. 2009 14:12 — Editoval musixx (02. 10. 2009 14:14)
Re: Omezení sumy čísel -> omezení jejich maxima
↑ Marian: Tohle řešení bohužel podle mě obsahuje stejný nedostatek, jakého jsem se dopustil výše. Nerovnost  očekává
očekává  . Klidně může být
. Klidně může být  , ale nějaké
, ale nějaké  . A pak detail: v definici
. A pak detail: v definici  se má jít asi přes všechna
se má jít asi přes všechna  , ne? Nebo jsem se v tomto vlákně spálil už podruhé?
, ne? Nebo jsem se v tomto vlákně spálil už podruhé?
Offline
#7 02. 10. 2009 17:35
- check_drummer

- Příspěvky: 4650
- Reputace: 101
Re: Omezení sumy čísel -> omezení jejich maxima
↑ check_drummer:
Tak jsem se zamyslel podruhé a je tu druhý díl úvah. :-) Případ n=4 máme dokázán. Zkusme indukci: . Abychom mohli použít indukci, musí platit, že poslední pravá strana je větší než n-1, tj.
. Abychom mohli použít indukci, musí platit, že poslední pravá strana je větší než n-1, tj.  .
.
Podobně, i když trochu zdlouhavěji dokážeme, že abychom mohli použít indukci, musí z druhé podmínky (se čtverci) platit:  a jelikož pro kladnou hodnotu
a jelikož pro kladnou hodnotu  bychom dostali, že
bychom dostali, že  , zabývejme se jen zápornými
, zabývejme se jen zápornými  , pak
, pak  .
.
Jelikož stačí, aby toto platilo pro libovolný index, nikoli n, stačí pro použití indukce najít jediné  splňující
splňující  .
.
Pokud takové i neexistuje, pokusím se dojít ke sporu, ale to až příště, teď mě tlačí čas, jako ostatně pořád. :-)
"Máte úhel beta." "No to nemám."
Offline
#8 03. 10. 2009 10:07
- check_drummer

- Příspěvky: 4650
- Reputace: 101
Re: Omezení sumy čísel -> omezení jejich maxima
↑ check_drummer:
Tak tu máme třetí pokračovaní. :-)
Tedy víme, že pro všechna  v této fázi důkazu platí, že
v této fázi důkazu platí, že  . Tedy buď je a_i kladné a větší než 1 a nebo záporné a menší než
. Tedy buď je a_i kladné a větší než 1 a nebo záporné a menší než  . Pro tuto chvíli předpokládejme, že záporná
. Pro tuto chvíli předpokládejme, že záporná  jsou rovna přesně
jsou rovna přesně  . (To je sice zjednodušení i nepřesnost, protože pro záporná
. (To je sice zjednodušení i nepřesnost, protože pro záporná  platí, že jsou ostře meší než
platí, že jsou ostře meší než  . Toto budeme muset v budoucnu ještě dořešit.) Označme jako "a" počet záporných
. Toto budeme muset v budoucnu ještě dořešit.) Označme jako "a" počet záporných  a tedy (n-a) je počet kladných
a tedy (n-a) je počet kladných  . Podle podmínek pro
. Podle podmínek pro  dostáváme (z druhé podmínky - se čtverci):
dostáváme (z druhé podmínky - se čtverci):  , tj.
, tj.  . Obdobně podle první podmínky:
. Obdobně podle první podmínky:  , tj.
, tj.  . Ovšem porovnáním obou podmínek pro a dostneme:
. Ovšem porovnáním obou podmínek pro a dostneme:  , tj.
, tj.  , z čehož ovšem po umocnění plyne
, z čehož ovšem po umocnění plyne  , což je ovšem splněno jen pro n<5 (a indukci uvažujeme pro n>=5). To je spor.
, což je ovšem splněno jen pro n<5 (a indukci uvažujeme pro n>=5). To je spor.
Zbývá dořešit problém, co když bude  libovolné záporné menší než
libovolné záporné menší než  a nikoli přesně rovno
a nikoli přesně rovno  . O tom ale snad někdy příště, pokud mě něco napadne. :-)
. O tom ale snad někdy příště, pokud mě něco napadne. :-)
"Máte úhel beta." "No to nemám."
Offline
#9 04. 10. 2009 17:19 — Editoval Rumburak (05. 10. 2009 12:22)
Re: Omezení sumy čísel -> omezení jejich maxima
Šel jsem na to následovně -
Offline
#10 05. 10. 2009 14:06
#11 05. 10. 2009 23:14
- check_drummer

- Příspěvky: 4650
- Reputace: 101
Re: Omezení sumy čísel -> omezení jejich maxima
↑ check_drummer:
Tak jsem na to šel nakonec sporem: dokážeme, že pro  nebude mezi
nebude mezi  žádné záporné číslo a zbytek bude snadný.
žádné záporné číslo a zbytek bude snadný.
Platí tedy:  , tedy
, tedy  , kde
, kde  je počet nekladných
je počet nekladných  , obdobně
, obdobně  . Označme pro
. Označme pro  :
:  , pak
, pak  a
a  . Umocnění první rovnosti na druhou dá:
. Umocnění první rovnosti na druhou dá:  . Nyní využijeme známou nerovnost, jejíž jméno jsem zapomněl :-) (cachy-schwarzova?):
. Nyní využijeme známou nerovnost, jejíž jméno jsem zapomněl :-) (cachy-schwarzova?):  .
.
Teď dáme vše dohromady:  , tj.
, tj.  , tj.
, tj.  a protože nemůže nastat a=n (všechna záporná čísla by nesplňovala první podmínku), můžeme nerovnici dělit (a-n) což je záporné číslo, tedy dostaneme a<1, což znamená, že všechna
a protože nemůže nastat a=n (všechna záporná čísla by nesplňovala první podmínku), můžeme nerovnici dělit (a-n) což je záporné číslo, tedy dostaneme a<1, což znamená, že všechna  jsou kladná. To ale znamená, že
jsou kladná. To ale znamená, že  (dle předpokladu, že
(dle předpokladu, že  a nyní navíc víme, že
a nyní navíc víme, že  ), tedy n < 4. což je spor s předpokladem, že n > 3 (n je celé).
), tedy n < 4. což je spor s předpokladem, že n > 3 (n je celé).
"Máte úhel beta." "No to nemám."
Offline
#12 06. 10. 2009 00:29
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Omezení sumy čísel -> omezení jejich maxima
Nerovnost  není Cauchy-Schwarzova, v MŘMÚ je uvedena jako speciální případ Jensenovy nerovnosti, ale ne té známé. Její platnost je ale po roznásobení zřejmá, takže není potřeba ji pojmenovávat.
není Cauchy-Schwarzova, v MŘMÚ je uvedena jako speciální případ Jensenovy nerovnosti, ale ne té známé. Její platnost je ale po roznásobení zřejmá, takže není potřeba ji pojmenovávat.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#13 07. 10. 2009 12:10
Re: Omezení sumy čísel -> omezení jejich maxima
Kondr napsal(a):
Myslím, že postačí úvaha o znaménkách.
...
Máme
z první nerovnosti, odtud
...
Myslím, že je tam překlep - citovaný odhad má mít tvar  . Ovšem pokud jsem zase cosi neřehlédnul.
. Ovšem pokud jsem zase cosi neřehlédnul.
Kondrova elementární úvaha je skutečně elegantní.
Offline
#14 07. 10. 2009 12:13 — Editoval musixx (07. 10. 2009 12:17)
Re: Omezení sumy čísel -> omezení jejich maxima
↑ Marian: Ano, a je tam ještě jeden na konci:  . A taktéž se připojuji k pochvale řešení.
. A taktéž se připojuji k pochvale řešení.
EDIT: Říkám si, jesli by nešlo se zbavit podmínky  (a zesílit současně tvrzení) tím, že budeme dokazovat, že
(a zesílit současně tvrzení) tím, že budeme dokazovat, že  . Ale moc jsem nad tím nepřemýšlel, takže je možné, že se najde lehce protipříklad.
. Ale moc jsem nad tím nepřemýšlel, takže je možné, že se najde lehce protipříklad.
Offline
#15 07. 10. 2009 14:10
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Omezení sumy čísel -> omezení jejich maxima
↑ Marian:↑ musixx:Díky, máte pravdu, opraveno.
musixx napsal(a):
EDIT: Říkám si, jesli by nešlo se zbavit podmínky
(a zesílit současně tvrzení) tím, že budeme dokazovat, že
. Ale moc jsem nad tím nepřemýšlel, takže je možné, že se najde lehce protipříklad.
To bohužel ne. Jak jsme s Rumburakem dokázali (geometricky i "analyticky"), nerovnost  pro
pro  nebude platit pro případ
nebude platit pro případ  a
a  . Dovolím si takový drobný poznatek (ne ze své hlavy): ke studiu nerovností je dobré určit, kdy nastává rovnost. Je to dobrá indicie pro to, jak silné/slabé odhady si může člověk dovolit.
. Dovolím si takový drobný poznatek (ne ze své hlavy): ke studiu nerovností je dobré určit, kdy nastává rovnost. Je to dobrá indicie pro to, jak silné/slabé odhady si může člověk dovolit.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé středoškolské úlohy
- » Omezení sumy čísel -> omezení jejich maxima (TOTO TÉMA JE VYŘEŠENÉ)
 ani potřeba.
ani potřeba. platí právě tehdy, když platí implikace
platí právě tehdy, když platí implikace  . No a pro
. No a pro  máme
máme  pro
pro  .
.



 .
.  , kde
, kde ,
,  .
.![kopírovat do textarea $X \,=\,[\,x_1,\,x_2,\,...\,,\,x_n\,]\,\in\,\mathbb{R}^n$](/mathtex/49/4998ab76b75fe31e91020c291523ee47.gif)
 , kde
, kde ![kopírovat do textarea $O \,=\,[\,0,\,0,\,...\,,\,0\,]\,\in\,\mathbb{R}^n$](/mathtex/b1/b13a3a0d65c86efde11d80d28e7420e9.gif) .
.  splňující (2) definujme
splňující (2) definujme  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
. označme
označme  její hranici v
její hranici v  její vnitřek v
její vnitřek v  ,
, její konvexní obal v
její konvexní obal v  .
.  ,
,  ,
,  ,
, .
. .
. .
. . Ta je jistě konvexní, neboť je průnikem množin, které jsou zřejmě konvexní rovněž:
. Ta je jistě konvexní, neboť je průnikem množin, které jsou zřejmě konvexní rovněž: je průnikem poloprostorů určených nerovnicemi
je průnikem poloprostorů určených nerovnicemi  ,
,  je nadrovinou v
je nadrovinou v  bodu
bodu  platí
platí  a dále
a dále  , z čehož
, z čehož  .
.![kopírovat do textarea $A_1 = [\,2-n,\, 2,\, ...\,, \,2\,]$](/mathtex/49/493d84c83a76871e15c5c01296699b6d.gif) ,
, ![kopírovat do textarea $A_2 = [\,2, \,2-n, \,2,\, ...\,,\, 2\,]$](/mathtex/85/85e13c01f6a15952ff78097b0f00a51c.gif) , ... ,
, ... , ![kopírovat do textarea $A_n = [\,2, \,\,...\,,\, 2, \,2-n\,]$](/mathtex/07/07d7bde0f68b673af44840dc006e62d0.gif) ,
, , takže
, takže  .
.![kopírovat do textarea $X \,=\,[\,x_1,\,x_2,\,...\,,\,x_n\,]\,\in\,M\,\cap\,\,\partial P$](/mathtex/77/770ed551249a7345095ac7d95bda3403.gif) , pak přímým výpočtem snadno ukážeme, že
, pak přímým výpočtem snadno ukážeme, že 
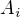 . Celkem tedy máme
. Celkem tedy máme .
. .
.![kopírovat do textarea $V \,=\,[\, 2,\, 2,\,...\,, \,2\,] \,\in\, \mathbb{R}^n$](/mathtex/05/05ecc21699d9697dabdb017d23053c7a.gif) , pak zřejmě
, pak zřejmě  . Dále
. Dále  , takže též
, takže též  .
. .
. k množině
k množině  zjistíme výpočtem jeho normy:
zjistíme výpočtem jeho normy:  (vzhledem k (1)). Pro
(vzhledem k (1)). Pro  , pro
, pro  je
je  .
. ,
,  ke "kouli"
ke "kouli"  plyne
plyne  ,
, , položme
, položme  . Kladná označme
. Kladná označme  , největší z nich označme M. Máme
, největší z nich označme M. Máme , odtud
, odtud 
 , tedy
, tedy , po úpravě
, po úpravě  . Pokud by všechna čísla byla kladná, je řešení snadné. Jinak
. Pokud by všechna čísla byla kladná, je řešení snadné. Jinak  a
a  .
.