Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Algoritmy a programování
- » Chybějící číslo(a) mezi 1 až n (TOTO TÉMA JE VYŘEŠENÉ)
#1 08. 10. 2009 21:26
- check_drummer

- Příspěvky: 5167
- Reputace: 106
Chybějící číslo(a) mezi 1 až n
Bratr mi dnes zadal úlohu: princezna má "n" korálků (které jsou očíslovány 1 až n) na šňůrce. Ta se však přetrhla a korálky se vysypaly. Našly se všechny kromě jednoho. Úkolem je co "nejjednodušeji" zjistit, který korálek chybí (jeho číslo). Ideálně: v konstantní paměti (resp. úměrné log(n)), jednoprůchodovým procházením seznamu nalezených korálků, v co nejkratším čase. Zobecnění: neztratil se jeden korálek, ale k.
Mé řešení:
"Máte úhel beta." "No to nemám."
Offline
#2 08. 10. 2009 21:47
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Chybějící číslo(a) mezi 1 až n
Offline
#3 11. 10. 2009 09:54
- check_drummer

- Příspěvky: 5167
- Reputace: 106
Re: Chybějící číslo(a) mezi 1 až n
"Máte úhel beta." "No to nemám."
Offline
#4 11. 10. 2009 10:51
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Chybějící číslo(a) mezi 1 až n
↑ check_drummer:K obecnému řešení: řešit soustavu umíme efektivně, pokud je to soustava lineárních rovnic. Proto bych uvažoval raději
.↑ BrozekP:Asi bylo míněno konstantní vzhledem k n. Pro pevné k lze do programu zadrátovat vzorce typu
 ,
, 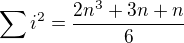 , atd. jejich složitost je (s využitím Hornerova schematu) O(k).
, atd. jejich složitost je (s využitím Hornerova schematu) O(k). BRKOS - matematický korespondenční seminář pro střední školy
Offline
#5 13. 11. 2009 18:44
- check_drummer

- Příspěvky: 5167
- Reputace: 106
Re: Chybějící číslo(a) mezi 1 až n
Kondr napsal(a):
↑ check_drummer:K obecnému řešení: řešit soustavu umíme efektivně, pokud je to soustava lineárních rovnic. Proto bych uvažoval raději
.
... Ovšem jakým způsobem uvedenou soustavu vytvořit? Resp. jak to zařídit, aby výsledný výraz měl hodnotu
? Myslím, že budu mít problém s ."Máte úhel beta." "No to nemám."
Offline
Stránky: 1
- Hlavní strana
- » Algoritmy a programování
- » Chybějící číslo(a) mezi 1 až n (TOTO TÉMA JE VYŘEŠENÉ)
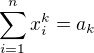
 jsou známy, budou tímto známy i příslušné koeficienty polynomu stupně k, tedy lze metodou pokusu a omylu vyzkoušet, která z čísel 1 až n jsou kořeny tohoto polynomu. Tím bude řešení dáno.
jsou známy, budou tímto známy i příslušné koeficienty polynomu stupně k, tedy lze metodou pokusu a omylu vyzkoušet, která z čísel 1 až n jsou kořeny tohoto polynomu. Tím bude řešení dáno.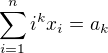
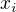 konkrétní hodnotou
konkrétní hodnotou 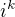 - zejména je problém s tím
- zejména je problém s tím 