Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 10. 10. 2009 12:24
Algebra - NSD
Ukažte, že v 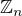 jsou prvky a, b asociované <=> NSD(a, n) = NSD(b, n)
jsou prvky a, b asociované <=> NSD(a, n) = NSD(b, n)
Prvky a, b jsou asociované pokud platí 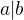 a zároveň
a zároveň 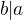 ("a | b" značí "a dělí b").
("a | b" značí "a dělí b").
Neporadil by mi s tím někdo?
EDIT: Moje úvaha ohledně implikace "=>":
Pokud bych byl v 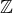 , pak by platilo toto:
, pak by platilo toto:
Máme NSD(a, n), protoze a|b => NSD(a, n) = SD(b, n) SD značí nějakého společného dělitele
protoze b|a => NSD(b, n) = SD(a, n)
Z toho dal: SD(a, n) <= NSD(a, n) <= SD(b, n) <= NSD(b, n) <= SD(a, n) => NSD(a, n) = NSD(b, n)
Lasciate ogni speranza. | Podílí se na Encyklopedii Fyziky (http://fyzika.jreichl.com) | Oblíbený IT projekt http://online-domain-tools.com
Offline
#2 12. 10. 2009 02:26
Re: Algebra - NSD
Myslim, ze tohle je uplne jasny, jestli to teda dobre chapu...
Co totiz znamena ze a|b (a deli b)?
To znamena, ze b je delitelny a nebo taky, ze b mod a = 0
Obracene b|a znamena, ze a je delitelny b nebo taky, ze a mod b = 0
Kdy jsou tyhle dve podminky splneny? No preci jenom kdyz a = b tim padem je jasny, ze ty dva prvky maji stejnyho NSD coz sou vlastne ty samotny prvky...
Jestli ti jde o ten vyraz NSD(a, n) = NSD(b, n) tak to je pak taky jasny...Kdyz a = b tak maji stejny rozklad na prvocisla a tim padem maji stejnyho NSD s jakymkoli jinym cislem...
Offline
#3 12. 10. 2009 08:30
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Algebra - NSD
↑ xxsawer:To bohužel není dobže, protože se pohybujeme v 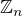 . Třeba v
. Třeba v 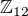 platí 5*5=1 a 5*1=5, proto 5|1 a 1|5. Na druhou stranu 2 nedělí 5.
platí 5*5=1 a 5*1=5, proto 5|1 a 1|5. Na druhou stranu 2 nedělí 5.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#4 13. 10. 2009 23:42
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Algebra - NSD
↑ Saturday:To NSD se musí brát v 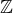 , jinak by nebylo jednoznačné. A pokud a|b v
, jinak by nebylo jednoznačné. A pokud a|b v 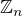 , pak v
, pak v 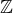
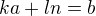 , takže opravdu NSD(a,n)=SD(b,n), tvůj důkaz je dobře.
, takže opravdu NSD(a,n)=SD(b,n), tvůj důkaz je dobře.
Druhá strana: NSD(a,n)=NSD(b,n)=d, n=de, a=df, b=dg. Nechť G je inverze g (mod e), z nesoudělnosti g a e takové G existuje. Pak
gG=te+1 , takže
, takže 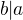 , symetricky dokážeme
, symetricky dokážeme 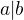 .
.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#5 18. 10. 2009 11:51
Re: Algebra - NSD
Díky moc!
EDIT:
Jeste zkusim rozpitvat tu mou implikaci, jestli jsem to dobre pochopil:
NSD tedy počítám v 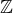 , pro c = NSD(a, n) mi tedy platí:
, pro c = NSD(a, n) mi tedy platí: 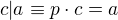 ,
, 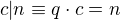 .
.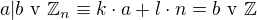
Abych ověřil, že c = SD(b, n), tak stačí ověřit, že platí c|b a c|n (toto už mám). 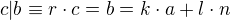 a za r můžu dosadit: k.p + l.q a rovnost platí => c|b.
a za r můžu dosadit: k.p + l.q a rovnost platí => c|b.
Je to dobře?
Lasciate ogni speranza. | Podílí se na Encyklopedii Fyziky (http://fyzika.jreichl.com) | Oblíbený IT projekt http://online-domain-tools.com
Offline