Matematické Fórum

marnes · 17. 10. 2009 19:21 — Editoval marnes (17. 10. 2009 19:21)

Dobrý den, potřeboval bych popostrčit s tímto příkadem. Vyřešte soustavu:
$x+y\ge 9$
$x+3y\ge 15$
$f_(min) =5x+2y$

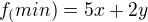
Ty první dvě nerovnice jsou mi jasné. Grafické řešení, vytvoření předpisu hraniční přímky, určení poloroviny řešení. Ale ta poslední rovnice. Nikdy jsem se s tím nesetkal. Osobně si představuju něco jako omezní zdola, takže bych to přepsal na 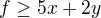$f\ge5x+2y$ .

Děkuji předem za odpověď

lukaszh · 17. 10. 2009 19:40

↑ marnes:
Mohol by si to nejako bližšie popísať, že pri akej teórii si sa s týmto stretol. Prípadne napísať, čo vyjadruje $f_{\rm{min}}$ . Priznám sa, že nechápem zadaniu.

marnes · 17. 10. 2009 19:44 — Editoval marnes (17. 10. 2009 19:46)

↑ lukaszh:
Nevím jestli to pomůže, ale napíšu doslovné znění:

Řešte graficky úlohy lineárního programování. Výsledek ověřte užitím řešitele excelu
$x+3y\ge 15$
$x+y\ge 9$
$f_(min) =5x+2y$

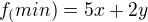
Nic víc:-(

Jinak pomáhám kámošce s řešením několika příkladů, jen tomuto také nerozumím. Zřejmě od ní budu muset vytáhnout nějakou teorii. Já jen jestli jste se s tím někdo nesetkal

jelena · 17. 10. 2009 19:51

↑ marnes: Zdravím srdečně, opětuji pozdrav z fyziky - ještě jsem neměla přiležitost zareagovat, ale snad...

K tomu dotazu: je potřeba minimalizovat funkci za stanovených podmínek - asi nejvíce toho mám napsáno tady: http://forum.matweb.cz/viewtopic.php?id=5022 i včetně stažení souboru pro Řešitel (nekde na závěr tématu).

Já ješte pohledam další témata, kde jsme něco podobného měli.

Ať se to podaří, připadně řekni, co je potřeba doplnit.

marnes · 17. 10. 2009 20:48 — Editoval marnes (17. 10. 2009 21:57)

↑ jelena:
Mnohokrát děkuji. Vzorové příklady jsem snad pochopil:-)

Kdyby ti zbylo trochu tvého drahocenného času a mohla mi zkontrolovat řešení, byl bych velice rád. Nespěchá:-)
$x+3y\ge 15$ prochází 5 tkou na y a 15 tkou na x - polorovina nahoru
$x+y\ge 9$ prochází 9 tkou na x i y - polorovina nahoru

průsečík v bodě 6;3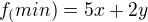

$f_(min) =5x+2y$ - základní prochází 2 kou na x a 5 tkou na y

A jestli mám teď vést rovnoběžku se základní nejblíže počátku, tak má tato rovnoběžka nekonečně mnoho společných bodů s řešením předcházejících nerovnic, takže nemá konečné optimální řešení ????

Vypadá to, že se mi i podařilo použít programy, na které jsi uvedla odkaz ( já jsem tak dobrej:-), na stará kolena se naučím pracovat s počítačem a programem v angličtině) a potvrdil mi mé řešení a i řešení druhého příkladu
$24\ge x+3y$
$42\ge 4x+3y$
$20\ge 2x+y$
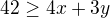
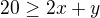
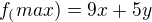$f_(max) =9x+5y$ kde závěr je x=9, y=2, z=91

Tak jen jestli by jsi zkontrolovala ten zápis řešení výsledku. Ještě jednou velké díky

jelena · 18. 10. 2009 19:42

↑ marnes:

Zdravím, moc se omlouvám, že odpovídám až teď - asi už máš všechno úspěšně vyřešeno.

Pro první zadání je potřeba vest rovnoběžku v krajních bodech oblasti nalevo (jelikož minimalizujeme):
na ose x (15, 0) nebo
v průsečíku (6, 3)
na ose y (0, 9)

Svůj růční nákres jsem ověřovala v programu, na který se odkazuji: vyšlo stejně:

(6,3) x+3y = 15; x+y = 9 36
(15,0) x+3y = 15; y = 0 75
(0,9) x+y = 9; x = 0 18 Minimum

Podařilo se vám vytvořit výpočet i v Řešiteli? Pokud bude něco potřeba, tak se ozví (i přes jiné komunikační prostředky - pokud bude potřeba přeposlat Řešitele).

Hezký zdraví Jelena.

marnes · 18. 10. 2009 21:37

↑ jelena:
Hlava vyvětraná, tvoje odpověď ůžasná a teď rychle zformulovat myšlenky.

Jestli to dobře chápu a nechci použít počítač:-) ( nejsme moc kamarádi), tak si ze zadaných nerovnic zjistím hraniční přímky, určím průsečíky těchto přímek, průsečíky s osami a tyto průsečíky dosadím do f (min) nebo f(max) a zjistím, kdy vychází největší nebo nejmenší hodnota?? Doufám že jsem to moc nezjednodušil.

Je to tak. Stačí ano - ne :-)

Ještě jednou velké díky. Matice, determinanty, limity, integrály, definiční obory už budou proti tomu hračka:-)

jelena · 18. 10. 2009 22:41 — Editoval jelena (18. 10. 2009 22:54)

↑ marnes:

marnes napsal(a):
tak si ze zadaných nerovnic zjistím hraniční přímky, určím průsečíky těchto přímek, průsečíky s osami a

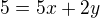zakresliš pomocnou přímku dle zadání účelové funkce: $z=5x+2y$ , například $5=5x+2y$ (pro x=0, y=2,5), (pro y=0, x=1) a k této přímce kresliš rovnoběžku v průsečíku přímek a v průsečíku přímek a os ( pokud minimalizuješ nemá smysl kreslit přes oblast, to už určitě bude více).

Ted dosazením x, y do z=5x+2y zjišťuješ, pro ktery z těchto bodů (který určitě patří oblasti a splňuje podmínky) vychází minimální hodnota účelové funkce z).

Ještě zde jsem optimalizovala, ale nejdou už stahovat soubory z uložiště (pokud bude potřeba, tak bych pohledala, kde to mám, byla to ruční tvorba).

Přerovská logistika, tipuji - hodně zdaru :-)

marnes · 18. 10. 2009 22:59 — Editoval marnes (18. 10. 2009 23:01)

↑ jelena:
Nechceš mi natipovat sportku?:-)

Ale vypadá to, že jsem v reálu. Však co, jednička to být nemusí:-) Děkuji.
P.S.: Kdybych tě měl za učitelku na výšce, tak by mě možná i bavila:-)

Matematické Fórum

#1 17. 10. 2009 19:21 — Editoval marnes (17. 10. 2009 19:21)

Dotaz

#2 17. 10. 2009 19:40

Re: Dotaz

#3 17. 10. 2009 19:44 — Editoval marnes (17. 10. 2009 19:46)

Re: Dotaz

#4 17. 10. 2009 19:51

Re: Dotaz

#5 17. 10. 2009 20:48 — Editoval marnes (17. 10. 2009 21:57)

Re: Dotaz

#6 18. 10. 2009 19:42

Re: Dotaz

#7 18. 10. 2009 21:37

Re: Dotaz

#8 18. 10. 2009 22:41 — Editoval jelena (18. 10. 2009 22:54)

Re: Dotaz

marnes napsal(a):

#9 18. 10. 2009 22:59 — Editoval marnes (18. 10. 2009 23:01)

Re: Dotaz

Zápatí