Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 23. 10. 2009 22:48
slovní úlohy
ahoj,
potřebovala bych pomoc s úloha z maturitních otázek, nějak mě nenapadá řešení.
1) Otec vyjel na chatu autem ráno v 7 hodin. V 7:30 za ním vyjel Jirka. Otec jel 48 km/hod. Jirka 60 km/hod. V kolik hodin se potkají? (vim, že to bude určitě triviální řešení, ale mně úlohy o pohybu nikdy nešly :( )
2) U rybníka jsou tři stavidla (2x přítok, 1x odtok). Je-li rybník prázdný, může být vytažením prvního stavidla naplněn za 1 1/4 dne, druhým za 1 3/4 dne. Je-li plný může být třetím stavidlem vypuštěn za 3/4 dne. Za jak dlouho by se prázdný rybník naplnil, kdyby byla všechna stavidla otevřena?
Děkuju moc za případnou pomoc :)
Offline
#2 23. 10. 2009 22:52 — Editoval Tychi (23. 10. 2009 22:53)
Re: slovní úlohy
↑ 007Misak:1)Když se potkají tak mají za sebou stejnou dráhu. Dráha se spočte jako 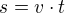 .
.
Dráha otce je  , dráha syna je
, dráha syna je  .
.
Vesmír má čas.
Offline
#3 23. 10. 2009 23:01 — Editoval Cermix (23. 10. 2009 23:01)
Re: slovní úlohy
takže první příklad:
Je třeba si uvědomut že tatík a Jirka (mimochodem můj jmenovec :-) ) urazí STEJNOU dráhu tudíž 
tatík jede rychlostí 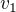 po dobu
po dobu 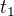 Jirka jede rychlostí
Jirka jede rychlostí 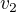 po dobu
po dobu 
dáme si rovnost s1 a s2

dále víme že Jirka vyrazil o půl hodinky POZDĚJI než táta. takže  To se dosadí do rovnice a výjde:
To se dosadí do rovnice a výjde:




to je doba po kterou jel tatík a to přičteš k času odjezdu a máš výsledek. Setkají se v 9:30 :-)
Žádné experimentování byť sebevíc intenzivní nedokáže, že mám pravdu, ale jediný experiment však může prokázat, že se mýlím.
Albert Einstein
Offline
#4 24. 10. 2009 08:03
Re: slovní úlohy
↑ 007Misak:
Druhá - to je na společnou práci.
Za 1 den se prvním stavidlem naplní  rybníka
rybníka
(To je snad jasné, kdyby se zalpnil např. za dva dny, tak za jeden de by to byla polovina rybníka.
Vždy je to 1/čas)
Za 1 den se druhým stavidlem naplní  rybníka
rybníka
Za 1 den třetím stavidlem odteče  rybníka
rybníka
Pokud se při všech třech otevřených stavidlech naplní za  dní, tak za jeden den je to
dní, tak za jeden den je to  rybníka
rybníka
Celková bilance za 1 den je proto
A  už vypočítáš.
už vypočítáš.
Pořádek je pro blbce, inteligent zvládá chaos!
Offline

