Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Střední škola
- » Rozložení kvadratického trojčlenu na součin lineárních (TOTO TÉMA JE VYŘEŠENÉ)
#1 25. 10. 2009 19:13
Rozložení kvadratického trojčlenu na součin lineárních
ahoj,
potřebovala bych radu, hlavně co se týče zadání: Rozložtě kvadratické trojčleny na součin lineárních, zapiště, kdy má výraz smysl a zjednodušte
A)
(4x^2+7x-2)/(12x^2+5x-2)
díky moc ...de mi taky o postup ... mám tu totiž ještě jeden příklad, kterej vypadá už trochu hůř :).
Offline
#2 25. 10. 2009 19:27 — Editoval Honza Matika (25. 10. 2009 20:45)
- Jan Jícha

- Veterán

- Místo: Plzeň/Mnichov
- Příspěvky: 1801
- Škola: ZČU - FST - KMM
- Pozice: Safety Engineer
- Reputace: 74
- Web
Re: Rozložení kvadratického trojčlenu na součin lineárních
Využijeme diskriminantu a poté viethových vztahů.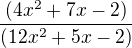
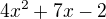
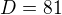
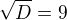
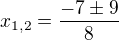
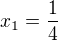
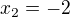
Využiju vietha a to je: 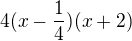
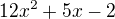
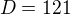
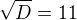
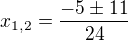
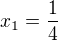
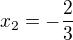
A vieth 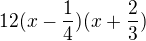
Takže zlomek: 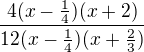
Tedˇvykrátím. A výsledek. 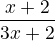
Zkoušku můžu provést tak, že do zadání si za x dosadín například 2.
A pak tu 2 dosadím i do výsledku, v obouch případech nám vyjde 
Výraz má smysl když: 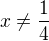 a
a 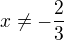
Můžeš napsat i ten těžší, kdybys nevěděl.
Offline
Stránky: 1
- Hlavní strana
- » Střední škola
- » Rozložení kvadratického trojčlenu na součin lineárních (TOTO TÉMA JE VYŘEŠENÉ)