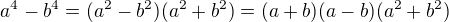Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 28. 10. 2009 00:00
výrazy a vzorce
ahoj,
počítala jsem 3. maturitní okruh - Odkaz a potřebovala bych zkontrolovat a případně i poradit s pár příkladama.
1 - e) mně to vyšlo 3x+1/(1-3x)^2, ale ve výsledkách bylo 3x-1/-9x^2+1 ale to nevim, jak na to přišli
2 - b) mi vyšlo n+2/n-2, ale výsledek byl zas jinej - n+2/9(n-2)^5
c) tak to mi nevyšlo vůbec, protože jsem nevěděla, co s 8x^3-1
3 - to jsme počítaly s učitelem a ten nechal jako výsledek (x-2)(x^2-1)/(x+2)(x^2-1),
ale já nevim, jestli by tam nemělo bejt (x-2)^2 a pak (x+2)^2
4 - c) mi vyšlo -2sgr(2)-1/sgr(2)-2 ale jako výsledek je uváděný 3+2sgr(2), což bude nejspíš správně, ale nevim, jak na to přišli
d) mi vyšlo 11-6sgr(2)/34-24sgr(2), ale to bude nejspíš taky blbost
Kdyby jste byl někdo tak ochotnej a kouknul na to, tak bych byla moc vděčná. Píšu na to v pondělí písemku a nevim, jak ji napíšu, když ani nevim, jak na to :(
Offline
#2 28. 10. 2009 08:57 — Editoval Doxxik (30. 10. 2009 13:05)
Re: výrazy a vzorce
↑ 007Misak:
2-b:
vyšlo mi taky 
2-c:  a tedy si můžeš rozložit:
a tedy si můžeš rozložit: podle vzorce
podle vzorce 
3 - to jsme počítaly s učitelem a ten nechal jako výsledek (x-2)(x^2-1)/(x+2)(x^2-1),
mno vyšlo mi to: { , pak by čitatel i jmenovatel šel pokrátit
, pak by čitatel i jmenovatel šel pokrátit  .. tedy výsledek:
.. tedy výsledek: 
4c: nejprve dáš oba zlomky na stejný jmenovatel a sečteš čitatele
a sečteš čitatele  .. dál se zbavíš odmocniny ve jmenovateli a to rozšířením na rozdíl čtverců (a^2 - b^2), získáš tedy:
.. dál se zbavíš odmocniny ve jmenovateli a to rozšířením na rozdíl čtverců (a^2 - b^2), získáš tedy:  /
/ =
=  /
/ .. a teď bych všchno umocnil ^2:
.. a teď bych všchno umocnil ^2:  /
/ v čitateli využiješ součtový vzorec:
v čitateli využiješ součtový vzorec:  /
/ dále v závorce v čitateli sečteš a pak vytkneš 2:
dále v závorce v čitateli sečteš a pak vytkneš 2:  /
/ a zkrátíš čitatel i jmenovatel 2. Zbude ti tedy
a zkrátíš čitatel i jmenovatel 2. Zbude ti tedy  /
/ a po roznásobení zísáš:
a po roznásobení zísáš: /
/
Doxxik
Offline
#3 28. 10. 2009 09:25
Re: výrazy a vzorce
↑ 007Misak:
1e) 


To je stejný výsledek jako uvádějí tvé výsledky, jen je ještě zkrácený
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#4 28. 10. 2009 09:36
Offline
#6 28. 10. 2009 09:43
Re: výrazy a vzorce
↑ 007Misak:
3. Je to jak píše Doxxik. Výraz
3a) pro  ,
, 
3b) 
3c) 
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#7 28. 10. 2009 09:53 — Editoval zdenek1 (28. 10. 2009 09:55)
Re: výrazy a vzorce
↑ 007Misak:
4c) Viz Tychi 
4d) Viz Tychi
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#8 28. 10. 2009 13:02
Re: výrazy a vzorce
všem moc děkuju, už mi to vychází a docela jsem to pochopila, což je nejhlavnější :)
akorát se furt plácám s tim 2c... i když jsem rozložila to 8x^3-1, tak mi to dál furt nevychází, tak kdybyste měl ještě někdo tolik trpělivosti a rozepsal mi to, tak bych byla moc ráda :)
a ještě jednou díky
Offline
#9 28. 10. 2009 14:26 — Editoval zdenek1 (28. 10. 2009 17:00)
Re: výrazy a vzorce
↑ 007Misak:2c) Nejprve jenom hranatou závorku
Výraz  jsem nejprve rozložil, abych mohl dát zlomky na společného jmenovatele a pak jsem to zase složil, abych se s tím furt nemusel opisovat.
jsem nejprve rozložil, abych mohl dát zlomky na společného jmenovatele a pak jsem to zase složil, abych se s tím furt nemusel opisovat. a nyní k tomu přidám ten zbytek
a nyní k tomu přidám ten zbytek ,
,  ,
, 
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#10 28. 10. 2009 16:43
Re: výrazy a vzorce
↑ zdenek1:Jen trošku mateš 8x je vždy na třetí ty máš chvilkama na druhou..
Vesmír má čas.
Offline

 ,
, 


 což se mi zdá jako hezké číslo a tedy správné
což se mi zdá jako hezké číslo a tedy správné