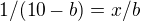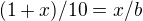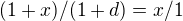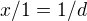Matematické Fórum

pusik1989 · 01. 11. 2009 18:47

U stěny leží krychlová bedna o hraně 1 m. U stěny stojí opřený desetimetrový žebřík, který se současně opírá o bednu. (viz obrázek).

Nu...a otázka zní: V jaké výšce v se žebřík opírá o stěnu?

Mé řešení

Autor skryl část textu. Zobrazit/skrýt!

halogan

To se pak ale nebude opírat o bednu. Kolega matoxy mě ale přivádí na myšlenku, že by mohl žebřík stát i obráceně - prostě jako kdybychom ze země udělali stěnu a ze stěny podlahu. Nějak to neumím vyjádřit.

Jdi na to přes podobnost trojúhelníků, máš tam 3 takové podobné.

Autor skryl část textu. Zobrazit/skrýt!

matoxy · 01. 11. 2009 19:05

Ak dobre chápem zadaniu tak vzdialenosť toho bodu čo je od zmeme 1m je aj od steny 1m. Čiže si to môžeme predstaviť tak, že ten rebrík sa okolo toho bodu môže vlastne otáčať a zeme a steny sa bude dotýkať práve vtedy, keď bude natočený pod určitým uhlom.
Tento uhl by sa dal nejak spočítať z tých trojuholníkov čo sú tam a nejakých sínusov cosínusov...

Jan Jícha · 01. 11. 2009 19:18

Řešilo se ZDE

Doxxik · 01. 11. 2009 20:10

pusik1989 napsal(a):
U stěny leží krychlová bedna o hraně 1 m. U stěny stojí opřený desetimetrový žebřík, který se současně opírá o bednu. (viz obrázek).

Nu...a otázka zní: V jaké výšce v se žebřík opírá o stěnu?

http://forum.matweb.cz/upload/1257097433-z.jpg

Mé řešení

Autor skryl část textu. Zobrazit/skrýt!
Skrytý text:
přišel jsem na to v hospodě :) a řekl bych, že se tato ůloha nemá řešení, protože se nedá říct že ten žebřík bude zrovna takhle opřený může být mnohem víc prudší.

píšu semka (nechci oživovat ono starší téma): jde to podle mě velice jednoduše a reciproká rovnice je zbytečně složitá (i když je to jistě taky řešení).
Můj návrh řešení:
označím si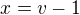
$x = v - 1$ (tedy výšku nad onou krychlí, ve které je opřen žebřík)
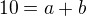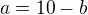$10 = a+b$ => $a = 10-b$ (a je vzdálenost na žebříku od země po bod, ve kterém se dotýká krychle + b je vzdálenost na žebříku od krychle po stěnu)
$d$ jako vzdálenost dotyku žebříku země a kraje krychle.
a dál bych použil jenom goniometrické funkce, protože ony dva trojúhelníky jsou jistě podobné, tedy jejich příslušné úhly jsou stejné.. a tedy:

$sin(alfa) = 1/(10-b)$
$sin(alfa) = x/b$
$sin(alfa) = (1+x)/10$
$tg(alfa) = (1+x)/(1+d)$
$tg(alfa) = 1/d$
$tg(alfa) = x/1$
$cos(alfa) = d/10$
$cos(alfa) = 1/b$
$cos(alfa) = (1+d)/10$

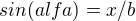
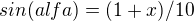
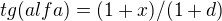
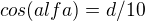
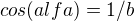
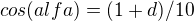
mno takže máme soustavu celkem 9 rovnic o 4 neznáých(x,d,b,alfa; resp. + sin,cos,tg), takže by soustava měla jít bez problémů vyřešit..

Doxxik

pusik1989 · 01. 11. 2009 20:40

↑ Doxxik:
myslím že szímhle bych měl problemy to vypočítat.

Doxxik · 01. 11. 2009 20:53 — Editoval Doxxik (01. 11. 2009 21:00)

i když si z toho uděláš rovnice:
sin(alfa):
$1/(10-b) = x/b$
$1/(10-b) = (1+x)/10$
$(1+x)/10 = x/b$
tg(alfa):
$(1+x)/(1+d) = 1/d$
$(1+x)/(1+d) = x/1$
$x/1 = 1/d$
cotg(alfa):
$d/10 = 1/b$
$d/10 = (1+d)/10$
$1/b = (1+d)/10$

kde jsou jen 4 neznámé.. a opět máš soustavu až 9 rovnic o 4 neznámých (ne?)

Doxxik

edit: vlastně jen 3 neznámé: x,b,d

pusik1989 · 01. 11. 2009 20:55

↑ Doxxik:
nikdy jsme nepočítal soustavu 9 rovnic maximalne 3 o trech

Doxxik · 01. 11. 2009 20:59

↑ pusik1989:
ee, já jsem nemyslel ani tak soustavu 9 rovnic o 3 neznámých (špatně jsem se vyjádřil), jako spíš že si můžeš vybrat libovolné rovnice (minimálně 3) z daných 9 rovnic, abys mohl spočítat dané 3 neznámé.. to že ti vztah určuje celkem 9 rovnic, to je výhoda pro tebe - vybereš si pouze ty, které se ti nejvíc hodí (nejlíp se ti s nimi bude počítat)

Doxxik

Matematické Fórum

#1 01. 11. 2009 18:47

Logická úloha, kdo pomůže?

#2 01. 11. 2009 18:58 — Editoval halogan (01. 11. 2009 19:14)

Re: Logická úloha, kdo pomůže?

#3 01. 11. 2009 19:05

Re: Logická úloha, kdo pomůže?

#4 01. 11. 2009 19:18

Re: Logická úloha, kdo pomůže?

#5 01. 11. 2009 20:10

Re: Logická úloha, kdo pomůže?

pusik1989 napsal(a):

#6 01. 11. 2009 20:40

Re: Logická úloha, kdo pomůže?

#7 01. 11. 2009 20:53 — Editoval Doxxik (01. 11. 2009 21:00)

Re: Logická úloha, kdo pomůže?

#8 01. 11. 2009 20:55

Re: Logická úloha, kdo pomůže?

#9 01. 11. 2009 20:59

Re: Logická úloha, kdo pomůže?

Zápatí