Matematické Fórum

kudelka · 03. 10. 2009 23:36

Ahoj, mám problém s těmito logaritmy a nevím jak s tím hnout... budu všem vděčná

jelena · 04. 10. 2009 00:37

↑ kudelka:

1. levou stranu upravit na mocniny se základem 2/3, pravou upravit na log se zakladem 8 (podle predposledniho pravidla) $\log_84=\frac23$

2. $\log_3x^3=3\log_3x$ take podle pravidel pro log, substituce $\log_3x=y$ povede na kvadratickou rovnici.

3. upravit mocninu nad x a logaritmovat levou a pravou stranu log se zakladem 10.

Pozor na def. obory.

Pomohlo?

Kikča15

prosím poraďte mi někdo s těmito příklady
1. 3*(4 na x + 9 na x+1) = 2* (3 * 4 na x+1 – 0,25 * 9 na x+1)

2. 2 * 4 na x – 5 * 2 na x + 2 * 4 na x-1 = 0

Tychi · 04. 10. 2009 17:55 — Editoval Tychi (04. 10. 2009 17:58)

↑ Kikča15: co to má společného s tématem?
$2 \cdot 4x-5\cdot 2x + 2 \cdot 4x-1 = 0$
$8x-10x+8x-1=0$
$6x-1=0$
$6x=1$
$x=\frac 16$

Kikča15 · 04. 10. 2009 17:58

to ma byt exponencialni rovnice asik resena logaritmií

Tychi · 04. 10. 2009 17:59

No tak to to musíš zapsat jinak, takhle to vypadá dost lineárně.

Kikča15 · 04. 10. 2009 18:02

no už sem to přepsala prosím pomůžes mi s tím ??

Chrpa · 04. 10. 2009 18:59 — Editoval Chrpa (04. 10. 2009 19:06)

↑ Kikča15:
$3\left(4^x+9^{x+1}\right)=2\left(3\cdot 4^{x+1}-0.25\cdot 9^{x+1}\right)\nl3\cdot4^x+3\cdot 9^{x+1}=6\cdot 4^{x+1}-\frac{2\cdot 9^{x+1}}{4}\nl6\cdot 4^x+54\cdot 9^x=48\cdot 4^x-9\cdot 9^x\nl63\cdot 9^x=42\cdot 4^x\nl3\cdot 9^x=2\cdot 4^x\nl\left(\frac{9}{4}\right)^x=\frac 23\nl\left(\frac 32\right)^{2x}=\left(\frac 32\right)^{-1}\nl2x=-1\nlx=-\frac 12$

Zkoušku si proveď sama.
Jen upozorňuji:
$4^x$ pro $x=-\frac 12$ platí:
$4^{-\frac 12}=\frac{1}{\sqrt 4}=\frac 12$

Kikča15 · 04. 10. 2009 19:38

2. 2 * 4 na x – 5 * 2 na x + 2 * 4 na x-1 = 0

Tychi · 04. 10. 2009 19:51 — Editoval Tychi (04. 10. 2009 19:54)

↑ Kikča15: A sama to nezkusíš?
$2\cdot 4^x-5\cdot 2^x+2\cdot 4^{x-1}=0$
$2\cdot 2^{2x}-5\cdot 2^x+2\cdot 2^{2x-2}=0$

PS.: Tyto rovnice nejsou logaritmické, ale exponenciální.

Ivana · 04. 10. 2009 20:07

↑ Kikča15:↑ Tychi:

Zdravím :-) , mohu se přidat ? :

Autor skryl část textu. Zobrazit/skrýt!

Tychi · 04. 10. 2009 20:17

↑ Ivana: Klidně se přidej, jak jsem si tak prohlédla příspěvky Kikči15, tak mi došlo, že asi nemá cenu snažit se, aby počítala něco sama, tak už jsem to řešení ani nemusím psát(o:

midmar · 02. 11. 2009 19:40

Ahojky.. moc bych potřebovala poradit s jedním příkladem.. nevím si rady
logx + √logx =6
oba logaritmy jsou se základem 2 !!

Doxxik · 02. 11. 2009 19:50 — Editoval Doxxik (02. 11. 2009 19:51)

↑ midmar:
substituce: $\sqrt{logx} = a$

pak spočítáš kvadratickou rovnici: $a^2 + a - 6 = 0$
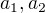vyjdou ti kořeny $a_1, a_2$ a z nich pak zjistíš: $a_1 = log{(x_1)}; a_2 = log{(x_2)}$

Doxxik

Matematické Fórum

#1 03. 10. 2009 23:36

logaritmy

#2 04. 10. 2009 00:37

Re: logaritmy

#3 04. 10. 2009 17:53 — Editoval Kikča15 (04. 10. 2009 18:00)

Re: logaritmy

#4 04. 10. 2009 17:55 — Editoval Tychi (04. 10. 2009 17:58)

Re: logaritmy

#5 04. 10. 2009 17:58

Re: logaritmy

#6 04. 10. 2009 17:59

Re: logaritmy

#7 04. 10. 2009 18:02

Re: logaritmy

#8 04. 10. 2009 18:59 — Editoval Chrpa (04. 10. 2009 19:06)

Re: logaritmy

#9 04. 10. 2009 19:38

Re: logaritmy

#10 04. 10. 2009 19:51 — Editoval Tychi (04. 10. 2009 19:54)

Re: logaritmy

#11 04. 10. 2009 20:07

Re: logaritmy

#12 04. 10. 2009 20:17

Re: logaritmy

#13 02. 11. 2009 19:40

Re: logaritmy

#14 02. 11. 2009 19:50 — Editoval Doxxik (02. 11. 2009 19:51)

Re: logaritmy

Zápatí