Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Algoritmy a programování
- » Funkce přibližně odpovídající obrázku (TOTO TÉMA JE VYŘEŠENÉ)
#1 02. 11. 2009 17:18
Funkce přibližně odpovídající obrázku
Ahoj,
řeším teď takový zajímavý problém pro který bych potřeboval najít vhodnou funkci.
Moje představa je funkce podobná té na obrázku:
Přičemž by se mi hodilo, kdyby měla dva parametry sigma1 a sigma2 (jsou vyznačené na obrázku). Moje představa je, že sigma1 by měnila, jak je rychle funkce klesá k nule v okolí 0 a sigma2 by měnila, v jaké absolutní vzdálenosti od 0 fce zase roste. Další podmínkou je, aby lim v +- nekonečnu byla stejná jako lim 0 (ideálně 1, ale to už si přenásobím). Na obrázku to není moc vidět, ale prostě aby už se od určité hodnoty větší než sigma2 chovala přibližně jako konstantní fce. Co by bylo také vhodné, aby byla „pro počítač rychle spočitatelná“, počet volání bude v řádech milionů a více.
Hledal jsem v příkladech gnuplotu (kde žádná vhodná není) a na http://functions.wolfram.com/ ale když člověk neví, jak se ta fce jmenuje, tak nemá šanci takovou najít.
Díky za jakékoliv nápady, ať už na to kde hledat, tak přímo na samotné fce.
Offline
#3 02. 11. 2009 19:47 — Editoval BrozekP (02. 11. 2009 19:55)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Funkce přibližně odpovídající obrázku
Použil bych součet těchto dvou funkcí: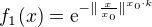

kde  bude vzdálenost od nuly, kde se to má začít zvedat/klesat, a
bude vzdálenost od nuly, kde se to má začít zvedat/klesat, a  bude úměrné tomu, jak rychlý růst/pokles to bude. Pro
bude úměrné tomu, jak rychlý růst/pokles to bude. Pro 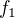 a
a 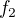 můžeš samozřejmě
můžeš samozřejmě  a
a  volit různě.
volit různě.
Takže např.
Offline
#4 02. 11. 2009 19:48 — Editoval stativ (02. 11. 2009 20:09)
Re: Funkce přibližně odpovídající obrázku
Lukee napsal(a):
?
To je právě problém, takhle jednoduchou funkci použít nemůžu, protože je:
1. periodická, já potřebuji aby od určité hodnoty byla +- konstantní
2. potřebuji, aby mezi prostředním „kopečkem“ a místem, kde opět začíná nabývat nenulových hodnot byla blízká 0.
Našel jsem fci, která splňuje většinu mých požadavků
ale ta bohužel není moc výpočetně výhodná… Prostřední část by se dala možná vyměnít za probability density function (netuším, jak se tomu česky říká).
Offline
#5 02. 11. 2009 19:54
Re: Funkce přibližně odpovídající obrázku
BrozekP napsal(a):
Použil bych součet těchto dvou funkcí:
kdebude vzdálenost od nuly, kde se to má začít zvedat/klesat, a
bude úměrné tomu, jak rychlý růst/pokles to bude. Pro
a
můžeš samozřejmě
a
volit různě.
Díky, tohle vypadá zajímavě, trošku si s tím pohraji a uvidím, co z toho vypadne. Nejspíš ale bude výpočet exp() rychlejší než atan(), už jenom proto, že se častěji používá, tak bude nejspíš lépe optimalizovaný.
Offline
#6 02. 11. 2009 20:11
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Funkce přibližně odpovídající obrázku
Probability density function (funkce hustoty pravděpodobnosti) může vypadat všelijak, asi jsi myslel tuto funkci pro normální rozdělení.
Offline
#8 02. 11. 2009 20:25
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Funkce přibližně odpovídající obrázku
↑ stativ:
Musí být spojitá? Diferencovatelná? Kolikátého řádu?
Offline
#9 02. 11. 2009 20:46
Re: Funkce přibližně odpovídající obrázku
BrozekP napsal(a):
↑ stativ:
Musí být spojitá? Diferencovatelná? Kolikátého řádu?
ad. Spojitá) No bylo by to lepší, chci ji použít na takovou „lepší“ klasifikaci pixelů
ad. diferencovatelná) Není třeba
ad. řád) To je vcelku fuk, ale aby se to rychle počítalo.
Ale vypadá to, že předchozí fce, co jsem psal je docela dobrá, úzké hrdlo je stejně pořád v nelineární diffuzi, takže i když se to počítá pomaleji, tak to není až taková prohra…
Offline
#11 02. 11. 2009 21:16
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Funkce přibližně odpovídající obrázku
↑ stativ:
Tak si tu funkci poskládej z několika málo lineárních funkcí - vytvoř lomenou čáru. Nebo je v tom nějaký problém?
Offline
#12 04. 11. 2009 19:09
Re: Funkce přibližně odpovídající obrázku
↑ BrozekP:
Mňo, pro okraje by to možná nebyl až takový problém, ale tohle funguje perfektně…
Offline
Stránky: 1
- Hlavní strana
- » Algoritmy a programování
- » Funkce přibližně odpovídající obrázku (TOTO TÉMA JE VYŘEŠENÉ)
