Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z algebry
- » Rozklady na součty čtverců (TOTO TÉMA JE VYŘEŠENÉ)
#1 30. 10. 2009 20:31
Rozklady na součty čtverců
Nechť c je přirozené číslo (nulu nepočítáme), navíc je c dělitelné nějakou mocninou dvojky, řekněme 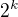 , kde k je nějaké přirozené číslo. Rozhodněte, jestli platí
, kde k je nějaké přirozené číslo. Rozhodněte, jestli platí .
.
kde a, b jsou přirozená čísla.
Offline
#2 02. 11. 2009 15:42
#3 02. 11. 2009 20:30 — Editoval Olin (02. 11. 2009 20:30)
Re: Rozklady na součty čtverců
Dnes během cesty ze školy mě ta indukce snad napadla:
Mám to dobře? :-)
Offline
#4 02. 11. 2009 23:05
#5 03. 11. 2009 21:32
Re: Rozklady na součty čtverců
OK, zkusím to trochu víc rozepsat.
Tvoje řešení je rozhodně hezčí, ale toto je snad taky správně, ne?
Offline
#6 03. 11. 2009 21:55
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4247
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Rozklady na součty čtverců
↑ Olin:Jo, tohle je OK. V původní verzi jsem moc nerozuměl tomu "Pak mají obě po dělení  zbytek
zbytek 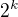 ", dávalo by mi tam smysl "Pak mají obě po dělení
", dávalo by mi tam smysl "Pak mají obě po dělení  zbytek
zbytek  ".
".
Moje řešení je s tím srovnatelné, jde o ten trik, že součet lichých kvadrátů nemůže být dělitelný 4.
Pozdravuju do Prahy :o)
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#7 04. 11. 2009 19:46
Re: Rozklady na součty čtverců
Ano, jak si to teď procházím, zjišťuji, že jsem napsal blbost (ale myslel jsem to dobře :-)
Pozdravuji do Brna :-)
Offline
#8 04. 11. 2009 21:46
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z algebry
- » Rozklady na součty čtverců (TOTO TÉMA JE VYŘEŠENÉ)


![kopírovat do textarea $\mathbb{Z}[i]$](/mathtex/6f/6f99ebfe6069982a3535bc0c6fe3690d.gif) je jedna ze závorek na levé straně dělitelná
je jedna ze závorek na levé straně dělitelná  v alespoň 2k-té mocnině, BÚNO
v alespoň 2k-té mocnině, BÚNO , po úpravě
, po úpravě , proto
, proto  ,
,  .
.
 , což je spor, protože má být
, což je spor, protože má být  .
.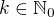 .
.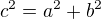 a
a  . Pak
. Pak  , protože jediný lichý kvadratický zbytek mod 4 je 1, musí být
, protože jediný lichý kvadratický zbytek mod 4 je 1, musí být 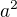 i
i  sudé (a dělitelné 4). Proto A=a/2,B=b/2 a C=c/2 splňují
sudé (a dělitelné 4). Proto A=a/2,B=b/2 a C=c/2 splňují  , dle indukčního předpokladu (a protože
, dle indukčního předpokladu (a protože  ) máme
) máme  ,
,  , proto
, proto  ,
,  , QED.
, QED. ,
, .
. , takže OK.
, takže OK. ,
, , tedy nemůže být.
, tedy nemůže být. ,
, , tedy nemůže být.
, tedy nemůže být.