Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » Cantorova množina (TOTO TÉMA JE VYŘEŠENÉ)
#1 08. 11. 2009 19:17 — Editoval Pavel (09. 11. 2009 18:31)
Cantorova množina
Nechť C je Cantorova množina. Určete C+C, kde sčítání dvou číselných množin je deffinováno takto:
EDIT: dvojtečka doplněna :-)
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#3 13. 11. 2009 09:51 — Editoval Rumburak (13. 11. 2009 14:51)
Re: Cantorova množina
Je to nakonec jednodušší, než jsem si původně myslel (neznal jsem to).
Offline
#4 19. 11. 2009 15:50
Re: Cantorova množina
↑ Rumburak:
To je přesně ono. Tak mě napadlo rozšířit tuto úlohu:
Najděte množinu ![kopírovat do textarea $D\subset[0,1]$](/mathtex/89/89be0c6a3f89035b9bf41d31628c4541.gif) takovou, že
takovou, že 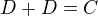 , kde
, kde  je Cantorova množina a sčítání množin je definováno obvyklým způsobem.
je Cantorova množina a sčítání množin je definováno obvyklým způsobem.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#5 21. 11. 2009 11:46 — Editoval Rumburak (24. 11. 2009 10:24)
Re: Cantorova množina
↑ Pavel:
Zdravím na Horní Bečvu a děkuji za další pěknou úlohu. I tentokrát byl Duch Svatý ke mně milostiv a osvítil mne . :-)
Offline
#6 26. 11. 2009 11:09 — Editoval Pavel (26. 11. 2009 11:10)
Re: Cantorova množina
↑ Rumburak:
Moc hezké řešení. Napadl, mě ještě jeden problém. Cantorova množina C je konstruována tak, že interval [0,1] se rozdělí na tří části a každá část znovu na tři části atd. Takže číslo 3 zde hraje důležitou roli. Tak co tak zkusit najít podmnožinu intervalu [0,1], označme ji opět D, takovou, že D+D+D=C. Zatím jsem nezkoumal otázku řešitelnosti, takže netuším, jak to vše vyjde :-)
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#7 27. 11. 2009 09:22 — Editoval Rumburak (01. 12. 2009 09:31)
Re: Cantorova množina
EDIT 1 : Ještě jsem opravil jednu chybu v předpokladech na množinu C.
EDIT 2 : Omlouvám se za zmatky, teď už je to snad definitivní.
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » Cantorova množina (TOTO TÉMA JE VYŘEŠENÉ)

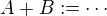 . Řešení znám, takže nechávám ostatním.
. Řešení znám, takže nechávám ostatním.![kopírovat do textarea $C + C = [0,\,2]$](/mathtex/67/677b9df623a6bf1769b44ebe95f0db0d.gif) .
.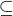 v (1) je zřejmá, neboť
v (1) je zřejmá, neboť ![kopírovat do textarea $C\subseteq[0,\,1]$](/mathtex/af/afd8622a723a753b7990558900afdafd.gif) .
.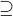 v (1) zvolme
v (1) zvolme ![kopírovat do textarea $z\in[0,\,2]$](/mathtex/08/08e2d28c2bddc8b16a23f35e816e49b1.gif) a nalezněme čísla
a nalezněme čísla 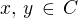 splňující
splňující 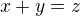 .
. 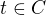 jsou charakterisována možností zapsat je ve tvaru
jsou charakterisována možností zapsat je ve tvaru 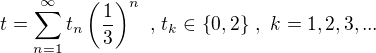 ,
,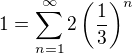 .
.![kopírovat do textarea $u \,:= \frac {z}{2}\in [0,\,1]$](/mathtex/fd/fd6500e022058bdc4a74405cb7ac2a70.gif) a vyjádřeme ho ve tvaru
a vyjádřeme ho ve tvaru 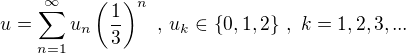 ,
,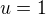 viz (3). Nyní definujme posloupnosti
viz (3). Nyní definujme posloupnosti 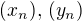 následovně:
následovně: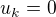 , pak
, pak 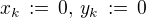 ,
,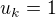 , pak
, pak 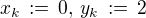 ,
,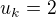 , pak
, pak 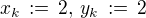 ,
,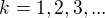 a položme
a položme 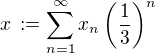 ,
, 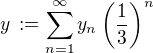 .
. 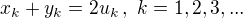 , proto
, proto 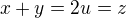 , přičemž čísla
, přičemž čísla 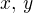 mají vlastnost (2) .
mají vlastnost (2) . bych ještě změkčil, formulace úlohy by pak vypadala takto:
bych ještě změkčil, formulace úlohy by pak vypadala takto: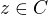 a pouze takovéto číslo lze vyjádřit ve tvaru
a pouze takovéto číslo lze vyjádřit ve tvaru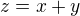 , kde
, kde 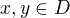 .
. 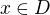 , pak číslo
, pak číslo 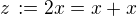 splňuje podmínku (2), proto
splňuje podmínku (2), proto ![kopírovat do textarea $z \in C \subseteq [0,\,1]$](/mathtex/bb/bbd842aaff48373db1b476dae6d8eba6.gif) , takže
, takže ![kopírovat do textarea $x = \frac {z}{2} \in [0,\,\frac {1}{2}]$](/mathtex/b9/b9befc307ed84ae4b71f248cf400d154.gif) , odtud
, odtud ![kopírovat do textarea $D \subseteq [0,\,\frac {1}{2}]$](/mathtex/5d/5ddfae4b7295cdc1954f0ce6a4fad111.gif) .
.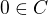 . Součet
. Součet 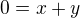 lze pro
lze pro ![kopírovat do textarea $x,y \in [0,\,\frac {1}{2}]$](/mathtex/d6/d646a3f0d9c23e1b2946ff757aa6ee1f.gif) realisovat jedině volbou
realisovat jedině volbou 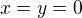 , takže aby platilo
, takže aby platilo 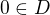 .
. 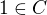 . Součet
. Součet 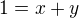 lze pro
lze pro 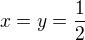 , takže aby platilo
, takže aby platilo 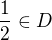 .
. 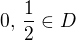 . Pak ale číslo
. Pak ale číslo 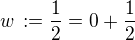 má vlastnost (2), tedy
má vlastnost (2), tedy 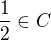 .
.![kopírovat do textarea $C \subseteq [0, \,1]$](/mathtex/18/180517ea7b1d3c96a8c4e4bb7440726f.gif) ,
, 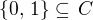 ,
, 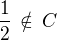 a obdrželi bychom týž výsledek.
a obdrželi bychom týž výsledek. 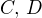 jsou číselné množiny splňující
jsou číselné množiny splňující ![kopírovat do textarea $ \{0,\,1\}\,\subseteq \,C \,\subseteq \,\[0,\,\frac{1}{3}\] \cup \[\frac{2}{3},\,1\] $](/mathtex/a6/a6f541edef1ef78e1e1d2cf0d7d6b480.gif) ,
, 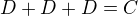 .
.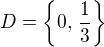 ,
, 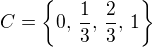 .
.![kopírovat do textarea $\{0,\,\frac{1}{3}\}\subseteq D \subseteq \[0,\,\frac{1}{3}\] $](/mathtex/fe/fef0a2da2fd205129d71e2e9a1edeb5a.gif) .
.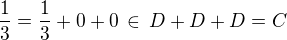 , podobně
, podobně 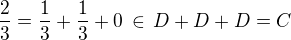 , takže
, takže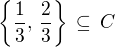 .
.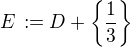 . Z (1) vyplývá
. Z (1) vyplývá ![kopírovat do textarea $\{\frac{1}{3},\,\frac{2}{3}\}\subseteq E \subseteq \[\frac{1}{3},\,\frac{2}{3}\] $](/mathtex/44/445218e6783d9107c13eb6070f7785ac.gif) . Zároveň
. Zároveň 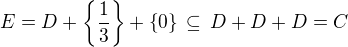 ,
, ![kopírovat do textarea $\{\frac{1}{3},\,\frac{2}{3}\}\subseteq E\,\subseteq\, \[\frac{1}{3},\,\frac{2}{3}\] \cap C= \{\frac{1}{3},\,\frac{2}{3}\}$](/mathtex/1d/1d54120b8545b28be43b8514bd7b4c41.gif) , odtud
, odtud 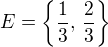 a zpětně
a zpětně 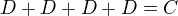 nemůže fungovat.
nemůže fungovat.