Matematické Fórum

scortyak47 · 13. 11. 2009 13:34

Dobry den pomohol by mi niekto s touto sustavou?
netusim ako to spocitat

m^3 = 27 (mod 55)
m^7 = 2 (mod 55)

--to = znamená je kongruentné
Vedeli by ste mi poradit ako dopocitam to m?
Vopred dakujem za odpoved.

Kondr · 13. 11. 2009 15:45

Pokud se to má řešit jako soustava, tak stačí umocnit první kongruenci na druhou a z ní do druhé dosadit za m^6 a ověřit výsledek, zjistíme, že žádné m nevyhoví.

Pokud řešíme každou zvlášť: z první kongruence máme 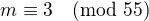$m\equiv 3\pmod{55}$ a ze druhé 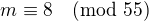$m\equiv 8\pmod {55}$ (řešíme zvlášť mod 5 a mod 11 a výsledek pak získáme z Čínské zbytkové věty).

scortyak47 · 13. 11. 2009 21:55

aha no viem ze riesenie by to malo mat, vedel by si mi napisat ako si vypocital jednotlive kongruencie? a pripadne niaku stranku kde to je popisane?

lukaszh · 14. 11. 2009 12:42

↑ scortyak47:
Veď ti to tam napísal. Skús na internete pohľadať Čínsku zvyškovú vetu. Prípadne v angličtine Chinese remainder theorem.

Matematické Fórum

#1 13. 11. 2009 13:34

Sustava kongruencii

#2 13. 11. 2009 15:45

Re: Sustava kongruencii

#3 13. 11. 2009 21:55

Re: Sustava kongruencii

#4 14. 11. 2009 12:42

Re: Sustava kongruencii

Zápatí