Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Limita Funkce ve vztahu k Limitě Posloupnosti (TOTO TÉMA JE VYŘEŠENÉ)
#1 16. 11. 2009 16:34
Limita Funkce ve vztahu k Limitě Posloupnosti
Zdravim, obracim se na vas s timto zrejme elementarnim problemem, ale jakkoli me mozkove zavity protacim nemuzu na to proste prijit, proste nedokazu pochopit jaktože posloupnost v tomto pripade konverguje k malemu "a", ktere lezi na ose x (to je na obrazku videt, ale hodnoty posloupnosti prece pokracuji i dale za to "a", takze tam prece nemuze konvergovat), spravne by mela konvergovat k tomu velkemu A, zda se mi ze je to uplne primitivni ale hlava mi to nejak nebere, dekuji za pomoc.
Zde je zneni inkriminovane Heineho vety (neni zas tak hrozny nepochopit dukaz ale nepochopit samotny zadani to uz je hodne spatny...)

Offline
#2 16. 11. 2009 19:06
Re: Limita Funkce ve vztahu k Limitě Posloupnosti
↑ RobbieMan:
ii) Uvažují se pouze ty posloupnosti, které konvergují k malému "a" a jejíž členy jsou od malého "a" různé. To je předpoklad. Pak platí, že posloupnost funkčních hodnot ve členech právě takových to posloupností konvergují k velkému "A".
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#3 16. 11. 2009 19:34
Re: Limita Funkce ve vztahu k Limitě Posloupnosti
a co teda znamena ze posloupnost konverguje k malemu "a" ? pak prece a=A...
uvedu priklad, napriklad funkce y=1/x konverguje k nule, stejne tak posloupnost An=1/n pro vsechna n prirozena, z cehoz snad plyne ze funkcni hodnota posloupnosti a funkce je prakticky stejna, akorat ze posloupnost ma "teckovany graf"...
Offline
#4 18. 11. 2009 11:57
Re: Limita Funkce ve vztahu k Limitě Posloupnosti
↑ RobbieMan:
Musíš rozlišovat mezi posloupnostmi  a
a 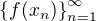 , kde f je předem daná funkce splňující výše uvedené vlastnosti. "a" je limita posloupnosti
, kde f je předem daná funkce splňující výše uvedené vlastnosti. "a" je limita posloupnosti  a "A" je limita posloupnosti
a "A" je limita posloupnosti 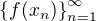 . Je-li např.
. Je-li např. 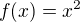 a
a 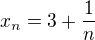 ,
, 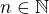 pak
pak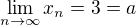 a
a
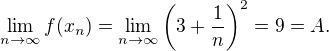
Zvolil jsem speciální posloupnost 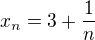 . Pokud budu uvažovat libovolnou posloupnost
. Pokud budu uvažovat libovolnou posloupnost  , která konverguje ke 3, a pokud bude příšlušná posloupnost
, která konverguje ke 3, a pokud bude příšlušná posloupnost 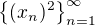 vždy konvergovat k 9, pak limitu posloupností mohu převést na limitu funkce a bude platit
vždy konvergovat k 9, pak limitu posloupností mohu převést na limitu funkce a bude platit
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Limita Funkce ve vztahu k Limitě Posloupnosti (TOTO TÉMA JE VYŘEŠENÉ)
