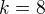Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 20. 11. 2009 22:52 — Editoval PitBull~--! (20. 11. 2009 22:54)
- PitBull~--!

- Příspěvky: 208
- Reputace: 0
binomicky rozvoj
Uz dlouho sem to nepocital a nevim jestli sem tenhle priklad spocital dobre.
zadani: koeficient u 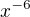 v binomickem rozvoji
v binomickem rozvoji ![kopírovat do textarea $(\sqrt[3]{x}-\frac12)^{10}$](/mathtex/29/29512f7725bc81b9e916911f344cda47.gif) .je roven cislo: me koeficient vyslo 10 nad 16/7-1 a to asi znamena ze nema reseni nebo neni reseni.
.je roven cislo: me koeficient vyslo 10 nad 16/7-1 a to asi znamena ze nema reseni nebo neni reseni.
___ ̴̡ı̴̡̡ *̡͌l̡*̡̡_*̡͌l̡*̡̡ ̴̡ı̴̴̡__ ̡̡͡|̲̲̲͡͡͡ ̲▫̲͡ ̲̲̲͡͡π̲̲͡͡ ̲̲͡▫̲̲͡͡ ̲|̡̡̡ ̡ ̴̡ı̴̡̡ *̡͌l̡*̡̡___
Offline
#3 20. 11. 2009 23:07
- PitBull~--!

- Příspěvky: 208
- Reputace: 0
Re: binomicky rozvoj
↑ Tychi:
ja sem tenhle priklad pocital podle tady toho prikladu http://web.quick.cz/koci.senior/Binom%20veta.htm
___ ̴̡ı̴̡̡ *̡͌l̡*̡̡_*̡͌l̡*̡̡ ̴̡ı̴̴̡__ ̡̡͡|̲̲̲͡͡͡ ̲▫̲͡ ̲̲̲͡͡π̲̲͡͡ ̲̲͡▫̲̲͡͡ ̲|̡̡̡ ̡ ̴̡ı̴̡̡ *̡͌l̡*̡̡___
Offline
#4 20. 11. 2009 23:12
Re: binomicky rozvoj
↑ PitBull~--!:
Fajn, ale nejspíš jsi blbě opsal zadání.
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#5 20. 11. 2009 23:32 — Editoval PitBull~--! (20. 11. 2009 23:34)
- PitBull~--!

- Příspěvky: 208
- Reputace: 0
Re: binomicky rozvoj
jo napsal jsem to blbe:) omlouvam se a hned to opravim.
tak zadani : koeficient u 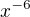 v binomickem rozvoji
v binomickem rozvoji ![kopírovat do textarea $(\sqrt[3]{x}-\frac2x)^{10}$](/mathtex/da/dab61777555aee9b3367ee7bc0de1660.gif) .je roven cislu
.je roven cislu
___ ̴̡ı̴̡̡ *̡͌l̡*̡̡_*̡͌l̡*̡̡ ̴̡ı̴̴̡__ ̡̡͡|̲̲̲͡͡͡ ̲▫̲͡ ̲̲̲͡͡π̲̲͡͡ ̲̲͡▫̲̲͡͡ ̲|̡̡̡ ̡ ̴̡ı̴̡̡ *̡͌l̡*̡̡___
Offline
#6 21. 11. 2009 08:12
Re: binomicky rozvoj
↑ PitBull~--!:
z rovnice 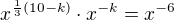 vypočítáš
vypočítáš 
Koeficient je pak 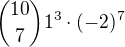
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#7 21. 11. 2009 11:00
- PitBull~--!

- Příspěvky: 208
- Reputace: 0
Re: binomicky rozvoj
koukni se prosim kde jsem udelal chybu?
___ ̴̡ı̴̡̡ *̡͌l̡*̡̡_*̡͌l̡*̡̡ ̴̡ı̴̴̡__ ̡̡͡|̲̲̲͡͡͡ ̲▫̲͡ ̲̲̲͡͡π̲̲͡͡ ̲̲͡▫̲̲͡͡ ̲|̡̡̡ ̡ ̴̡ı̴̡̡ *̡͌l̡*̡̡___
Offline
#8 21. 11. 2009 15:47
Re: binomicky rozvoj
↑ PitBull~--!:
Nikde nemáš chybu. Vypočítej  ze své poslední rovnice
ze své poslední rovnice
a pak ho dosaď zpět do tvého vzorečku (3. řádek Ak=....). Dostaneš úplně to samý co já.
Proč to dělat jednoduš, když to jde složitě?
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#9 21. 11. 2009 16:52
- PitBull~--!

- Příspěvky: 208
- Reputace: 0
Re: binomicky rozvoj
↑ zdenek1: aha, uz sem tu chybu nasel. Predim jsem to blbe vynasobil a nemoh sem to najit. :)
___ ̴̡ı̴̡̡ *̡͌l̡*̡̡_*̡͌l̡*̡̡ ̴̡ı̴̴̡__ ̡̡͡|̲̲̲͡͡͡ ̲▫̲͡ ̲̲̲͡͡π̲̲͡͡ ̲̲͡▫̲̲͡͡ ̲|̡̡̡ ̡ ̴̡ı̴̡̡ *̡͌l̡*̡̡___
Offline

 ), tak nikdy nemůžeš dostat
), tak nikdy nemůžeš dostat 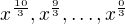 .
.