Matematické Fórum

Spybot · 20. 11. 2009 18:48

Zdravim, pomohli by ste mi prosim s tymto prikladom?

Osobný automobil A a za ním v tesnej vzdialenosti d1 = 20 m automobil B sa pohybujú rovnakou rýchlosťou v1 = 75 km.h-1. V okamihu, keď sa vodič automobilu B rozhodne predbiehať, objaví sa pred ním v protismere vo vzdialenosti d0 automobil C, pohybujúci sa rýchlosťou v2 = 90 km.h-1.

Pri akej vzdialenosti d0 bude predbiehanie bezpečné ?

Pri predbiehaní vyvinie automobil B zrýchlenie a1 = 0,25 m.s-2 a neprekročí maximálnu povolenú rýchlosť v2. Predbiehanie považujeme za bezpečné, ak sa automobil B zaradí pred A vo vzdialenosti d1 a súčasne je vzdialenosť automobilu C od B d = 50 m.

Aký by bol výsledok v prípade slabšieho vozidla pri zrýchlení a2 = 0,15 m.s-2 ?

Rozmery automobilov neuvažujte.

Vdaka za vas cas.

KennyMcCormick · 21. 11. 2009 13:21

↑ Spybot:
Při jaké vzdálenosti $d_0$ bude předjíždění bezpečné?

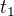$t_1$ čas, po který může automobil A zrychlovat, aniž by překročil povolenou rychlost
$s_1$ dráha, kterou automobil A urazí rovnoměrně zrychleným pohybem
$t_2$ čas, po který se bude automobil A pohybovat rovnoměrně přímočaře
$v_2=v_1+a_1t_1$
$s_1=0.5a_1t_1^2$
$2d_1-s_1=v_2t_2$
$d_0-2d_1-d=(t_1+t_2)v_2$

Dosadíš:
$25=\frac{125}6+0.25t_1$
$s_1=0.5*0.25t_1^2$
$2*20-s_1=25t_2$
$d_0-2*20-50=(t_1+t_2)25$

$d_0\approx511.94m$

Jaký by byl výsledek v případě slabšího vozidla při zrychlení $a_2=0.15ms^{-2}$

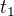$t_1$ čas, po který může automobil A zrychlovat, aniž by překročil povolenou rychlost
$s_1$ dráha, kterou automobil A urazí rovnoměrně zrychleným pohybem
$t_2$ čas, po který se bude automobil A pohybovat rovnoměrně přímočaře
$v_2=v_1+a_2t_1$
$s_1=0.5a_2t_1^2$
$2d_1-s_1=v_2t_2$
$d_0-2d_1-d=(t_1+t_2)v_2$

Dosadíš:
$25=\frac{125}6+0.15t_1$
$s_1=0.5*0.15t_1^2$
$2*20-s_1=25t_2$
$d_0-2*20-50=(t_1+t_2)25$

$d_0\approx766.57m$

Matematické Fórum

#1 20. 11. 2009 18:48

Kinematika

#2 21. 11. 2009 13:21

Re: Kinematika

Zápatí