Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 18. 11. 2009 11:38
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Kombinatorika
↑ zbynek:
Zdravím,
budoucí informatik by měl vědet, že pro to, aby vznikla odpověď, měla by být položena otázka - což v případě úvodního příspěvku v tématu není.
Tak já tedy položím otázku:
- je možné sestavovat i kratší slova, než osmipismenková?
- je možné pro vyloučení (například) nepovoleného slova AUTO použit tento postup _A_U_T_O_, mám tedy pěvně dany pozice pro uspořádání nepovolených pismen a na mezerý umístim ostatní pismena. Jak ošetřím, že na jednu mezeru mohu dat i více písmen?
Já opravdu nevím, proto jsou moje otázky - ale vy jste to možna měli ve cvičení.
Děkuji za doplnění a vysvětlení a doporučuji přečist si místní pravidla, zejména bod 4.
Offline
#3 19. 11. 2009 20:26
Re: Kombinatorika
Máme tvořit slova pouze osmipísmenková ;-)
Já bych to zkusil řešit tak, že bych si spočítal počet slov kdy písmeno A bude na 1. - 5. pozici tzn. A _ _ _ A _ _ _ . Písmeno A na 3.pozici by již nevytvořilo podslovo AUTO.
//
A U T O _ _ _ _
A _ U _ _ T O_
_ A U T O _ _ _
_ _ A U T O _ _
_ _ _ A U T O _
_ _ _ _ A U T O
+++ písmena U T O mohou bý jakkoliv seřazeny a na jakékoliv pozici za písmenem A
Poté počet slov kdy písmeno U bude na 2. - 6. pozici. Písmeno U na 1. , 7. a 8. pozici by nevytvořilo podslovo AUTO.
- || - písmeno T na 3. - 7. pozici.
- || - písmeno O na 4. - 8. pozici.
To stejné s podslovy RUKA a HOD.
R na 1. - 5. pozici.
U na 2. - 6. pozici.
K na 3. - 7. pozici.
A na 4. - 8. pozici.
H na 1. - 6. pozici.
O na 2. - 7. pozici.
D na 3. - 8. pozici.
...
Offline
#4 20. 11. 2009 14:04
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Kombinatorika
↑ dreek:
Zdravím a děkuji za příspěvek k problému (autor dotazu ovšem pořad nic?)
Při takovém "ručním" seřazení bych měla obavy, ať na nějakou pozici nezapomenu.
Ještě jen doplnění, ale to asi víš, že RUKA a AUTO v jednom slově spolu nebudou, ale RUKA a HOD nebo HOD a AUTO mohou se potkat v jednom slově (zejména HOD s AUTO - tak se to dokonce "přesmyčkuje"). Je to tak?
Offline
#5 20. 11. 2009 14:48
Re: Kombinatorika
↑ dreek:
Takže za předpokladu, že se tvoří osmipísmenná slova a každé písmeno použiju právě jednou.
Lepší počítání je: Vyberu čtyři pozice, na které umístím písmena AUTO. To můžu dělat 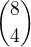 způsoby. Jakmile mám vybranou jednu takovou čtveřici, písmena umístím jednoznačně. Zbylá písmena na zbylých pozicích můžou libovolně permutovat. Takže slov, která obsahují podslovo AUTO je
způsoby. Jakmile mám vybranou jednu takovou čtveřici, písmena umístím jednoznačně. Zbylá písmena na zbylých pozicích můžou libovolně permutovat. Takže slov, která obsahují podslovo AUTO je 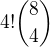
Ostatní podobně.
HOD 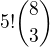
RUKA 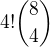
AUTO a RUKA 
AUTO a RUKA a HOD 
HOD a RUKA 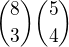 (vyberu 3 pozice pro HOD a pak 4 pozice ze zbytku pro RUKA)
(vyberu 3 pozice pro HOD a pak 4 pozice ze zbytku pro RUKA)
AUTO a HOD. Někam musím umísti sekvenci písmen 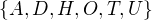 . Vyberu tedy 6 pozic
. Vyberu tedy 6 pozic  způsoby.
způsoby.
Jakmile je vyberu, jsou určeny _ _ _ _ O D. Nyní můžu čtyřmi způsoby umístit H. Jakmile to udělám, pozice písmen AUT je daná. Nakonec mi zbývají K R, ta mohou libovolně permutovat na 2 pozicích.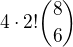
Nyní spočítáš podle principu inkluze a exkluze počet "HOD nebo AUTO nebo RUKA" a odečteš od počtu všech možných slov ( )
)
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#6 24. 11. 2009 21:11
Re: Kombinatorika
Děkuji za rady..
Prosím ještě o menší kontrolu ;)
výskyt podslov:
AUTO 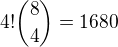
HOD 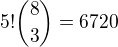
RUKA 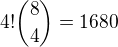
HOD A RUKA 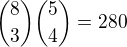
AUTO A HOD 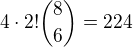
AUTO a RUKA 
AUTO a RUKA a HOD 
inkluze a exluze:
AUTO = |A| = 1680,
HOD = |B| = 6720,
RUKA = |C| = 1680,
HOD A RUKA = |B∩C| = 280,
AUTO A HOD = |A∩B| = 224,
AUTO A RUKA = |A∩C| = 0,
AUTO A HOD A RUKA = |A∩B∩C| = 0
|AUBUC| = |A| + |B| + |C| - |A∩B| - |A∩C| - |B∩C| + |A∩B∩C|
|AUBUC| = 1680 + 6720 + 1680 - 224 - 0 - 280 + 0
|AUBUC| = 9576
8! - 9576 = 30744
Můžeme tedy sestavit 30744 slov.
Offline
#7 30. 11. 2009 10:29 — Editoval dreek (30. 11. 2009 10:37)
Re: Kombinatorika
zbynek napsal(a):
Omlouvam se, za smazani nasledujiciho tematu, ale toto tema bylo zalozeno bez meho vedomi. Urcita osoba se nabourala do meho loginu a zalozila toto tema a ja si nepreji aby toto tema bylo zverejneno. Děkuji za pochopeni.
No to nevadí ;-)
Mi to téma dost pomohlo 8)
Pro ty, kdo hledají zadání..
Mějme písmena A,D,H,K,O,R,T,U. Kolik různých slov můžeme sestavit z těchto písmen, pokud tato slova nesmí obsahovat "podslova" AUTO, RUKA a HOD (například hAdUrTkO je nepřípustné slovo).
OT: jinak trošku tragédie Zbynku :D Založil sis účet 17.11.2009 a v ten den už ti ho někdo naboural a založil úplně nedůležité vlákno o kombinatorice :D pobavil jsi ;)
... ale jo, snad to tady všichni z VŠB neobjeví co? ;D
Offline
#10 03. 12. 2009 13:58
Re: Kombinatorika
Já bych vzal postup, propočítal to znova a jestli se shodnem na výsledku, třeba to bude dobře ;-)
Offline
