Matematické Fórum

miraul · 30. 11. 2009 16:07

mcdodo · 30. 11. 2009 17:27

prosím o popoc s tímto příkladem....

zdenek1 · 30. 11. 2009 17:35

↑ mcdodo:
A co nevíš?

mcdodo · 30. 11. 2009 17:48

bude to znít blbě, ale kopletně....netušim jak se tohle počítá... a taky to blbé je..:-(

zdenek1 · 30. 11. 2009 18:03

↑ mcdodo:
Slyšel jsi někdy o vodorovném vrhu?

mcdodo · 30. 11. 2009 18:06

↑ zdenek1:

vodorovný..??slyšel jsem o šikmém...o svislém..ale vodorovném ne...

Roman12 · 30. 11. 2009 18:15

↑ mcdodo:
čau, prosim Vás, máme problém s tímto příkladem. Je tam i chyba v zadání
(je špatně okótováno => že d=D=200mm a b=d=2m) beru to, že zadání je správně ;-)

Teď bych chtěl poprosit, zda by byl někdo ochoten nám s tímto příkladem pomoci.
Díky

zdenek1 · 30. 11. 2009 18:28

↑ Roman12:
Doba vrhu (vodorovného) je 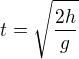$t=\sqrt{\frac{2h}g}$ .
Jenže to musíš počítat pro výšku těžište (středu) kluličky. TAkže to bude 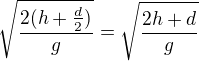$\sqrt{\frac{2(h+\frac d2)}g}=\sqrt{\frac{2h+d}g}$

Aby se dostala kulička k levému kraji, musí se střed kuličky dostat do vzdálenosti 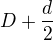$D+\frac d2$
Ve vodorovném směru se jedná o rovnoměrný pohyb, takže $tv_{min}=D+\frac d2$
$v_{min}=(D+\frac d2)\cdot \sqrt{\frac{g}{2h+d}}$

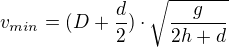
Když se má dostat k pravému okraji je vzdálenost 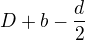$D+b-\frac d2$ , čas je stejný.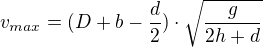
$v_{max}=(D+b-\frac d2)\cdot \sqrt{\frac{g}{2h+d}}$

Symboly používám tak, jak jsou v textu.

mcdodo · 30. 11. 2009 18:35

↑ zdenek1:

Děkuji...
ale takhle...mi to máme jako semestrálku na jeden předmět.. a všechny osattní zadaaní tam mají samé derivace integrali..tak že se mi moc nezdá že by tohle bylo řešení...jako ano..lze to takhle vypočítat...ale newim estli se od nás tohle očekává...

zdenek1 · 30. 11. 2009 18:46

↑ mcdodo:

No z těch 10-ti příkladů (soubor "priklady K.pdf") jsou na derivace je 4. Ostatní jsou této úrovně. Ale když si to chceš ztížit, klidně můžeš pomocí integrálů odvodit ten vztah pro dobu pádu.

Roman12 · 30. 11. 2009 18:48

no asi tak, ale zdenek1 - prosim tě, takhle jak jsi mi to spočítal to je proto, protože bude její střed v místě "měření" náležet s vodorovnou stěnou ;-) pomoc derivací a integrálů by byla nutná, kdyby ten otvor kam má spadnout byla mnohem dál než 20cm (z výšky 4m) - ale i tak je tam nějaký úhel přes hranu otvoru :o(

Nebo myslíš, že ne.
Díky Roman12

mcdodo · 30. 11. 2009 18:52

↑ zdenek1:
máš všechny ty příklady K-...??a proč teda tam máme zadanou tu hodnotu ay(y)= -9,81 m/s2 ..??

zdenek1 · 01. 12. 2009 14:56

↑ Roman12:
Tak jsem o tom přemýšlel a máš. pravdu. Ten způsob výše nedá nejmenší rychlost. Práce kvapná, málo platná

Nejmenší rychlost by měla být podle obrázku. V rohu si myslíš kruřnici se stejným poloměrem jako má kulička. A pak zvolíš takovou rychlost, aby trajektorie (parabola) byla tečnou myšlené kružnice. Bohužel mě nenapadá žádný jednoduchý způsob, jak to spočítat. Ale koneckonců, je to vaše práce.

Za předchozí mystifikaci se omlouvám

mcdodo · 02. 12. 2009 17:18

↑ zdenek1:
a nějaký složitý způsob by si tam neměl..???prosiim..

Matematické Fórum

#1 30. 11. 2009 16:07

kinematika

#2 30. 11. 2009 17:27

Re: kinematika

#3 30. 11. 2009 17:35

Re: kinematika

#4 30. 11. 2009 17:48

Re: kinematika

#5 30. 11. 2009 18:03

Re: kinematika

#6 30. 11. 2009 18:06

Re: kinematika

#7 30. 11. 2009 18:15

Re: kinematika

#8 30. 11. 2009 18:28

Re: kinematika

#9 30. 11. 2009 18:35

Re: kinematika

#10 30. 11. 2009 18:46

Re: kinematika

#11 30. 11. 2009 18:48

Re: kinematika

#12 30. 11. 2009 18:52

Re: kinematika

#13 01. 12. 2009 14:56

Re: kinematika

#14 02. 12. 2009 17:18

Re: kinematika

Zápatí