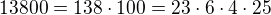Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 03. 12. 2009 19:48
Kombinatorika
Mám tu pár příkladů:
a) Kolika způsoby lze vybrat 3 výrobky z 10 výrobků?
b)Kolika způsoby lze vybrat z 100 výrobků 3 výrobky ke kontrole jakosti, je-li po kontrole výrobek vždy vrácen zpět?
c)Kolika způsoby může být 12 různých knih uspořádáno na poličce v knihovně?
d)Z kolika prvků lze vytvořit 13 800 variací třetí třídy?
Offline
#3 03. 12. 2009 20:27
Re: Kombinatorika
↑ ColePf:
Ještě k d). marnes ti napsal rovnici, ale ta je kubická a obtížně se řeší. Vezmi v úvahu, že na levé straně je součin tří po sobě jdoucích čísel. Rozlož si pravou stranu na prvočinitele a pokus se z nich sestavit ta tři zasebou jdoucí čísla. jde to velice snadno.
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#4 03. 12. 2009 20:41
Re: Kombinatorika
↑ zdenek1:
jak to prosím rozložím na prvočinitele?
e) Další který nevím:( Kolik prvků je zapotřebí k vytvoření 40320 permutací?
Offline
. Začni: vyděl 40320:2, výsledek vyděl 3, výdledek vyděl 4 atd.
#7 03. 12. 2009 20:57
Re: Kombinatorika
Omlouvám se, že mám další příklad. Zítra mám písemku a moje jediná slabina je kombinatorika:(
f) 8 pracovníku chce vyjádřit nespokojenost řediteli. Ředitel je ochotej přijmout tříčlennou delegaci. Kolika způsoby lze takovou delegaci vytvořit?
Offline
