Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Výpočet integrační oblasti u dvojného integrálu (TOTO TÉMA JE VYŘEŠENÉ)
#1 29. 01. 2008 18:11
Výpočet integrační oblasti u dvojného integrálu
Ahoj.
Mohl by mi prosím někdo stručně říci, jak si mám vypočítat meze dvojného integrálu přes základní oblast? Prostě, když mám zadáno, že oblast je omezená křivkou např.: |x|+|y|=1.
Konkrétně u tohoto příkladu. Když to vidím nakreslené, tak x je mezi -1 až 1. Tento útvar je symetrický podle osy x i y. Takže mi to stačí v prvním kvadrantu. A tam je x=0 až 1 a y=0 až 1-x.
Chápu, jak se dostalo 1-x, ale nevím, jak se přišlo na 0 u y.
A když bych měl např.: oblast omezenou křivkami y=2-x a y^2=4x+4, tak jsem si to nakreslil a x je mezi -1 až 3, ale nevím, jak dostat y?
Budu vděčný za každou radu.
Offline
#2 29. 01. 2008 18:52
Re: Výpočet integrační oblasti u dvojného integrálu
kdyz si nakreslis oblast 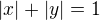 , tak dostanes kosoctverec (tohle je tedy dokonce ctverec pootoceny o 45 stupnu) se "stredem" v pocatku souradnic a delkou uhlopricky 2. pokud budes pocitat integral
, tak dostanes kosoctverec (tohle je tedy dokonce ctverec pootoceny o 45 stupnu) se "stredem" v pocatku souradnic a delkou uhlopricky 2. pokud budes pocitat integral 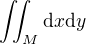 pres danou oblast, tak si muzes usetrit praci a spocitat jej pouze pro oblast v prvnim kvadrantu a vysledek vzit 4x. pokud ale budes pocitat integral
pres danou oblast, tak si muzes usetrit praci a spocitat jej pouze pro oblast v prvnim kvadrantu a vysledek vzit 4x. pokud ale budes pocitat integral 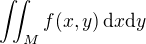 , tak to ale stejne jako v predeslem pripade udelat nelze, budes si muset danou oblast rozdelit, treba na dve takto: pro
, tak to ale stejne jako v predeslem pripade udelat nelze, budes si muset danou oblast rozdelit, treba na dve takto: pro 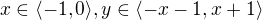 a pro
a pro 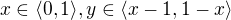 , vysledek je pak soucet dvou dilcich integralu pres tyto dve suboblasti.
, vysledek je pak soucet dvou dilcich integralu pres tyto dve suboblasti.
v druhem pripade je oblast ohranicena primkou a parabolou, spocitas si pruseciky x=0, x=8 a poradne si to namalujes a pak to opet rozdelis na podoblasti, treba 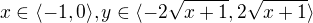 a
a 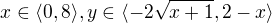
Offline
#3 29. 01. 2008 19:54 — Editoval jelena (29. 01. 2008 22:05)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Výpočet integrační oblasti u dvojného integrálu
Zdravim,
souhlasim s kolegou plisna, jen male upozorneni - az nakreslime grafy funkci a najdeme pruseciky, tak musime volit poradi x nebo y tak, aby funkce, co omezuji byly proste. Zkratka obrazek tocim "nalezato - nastojato".
Treba - v pripade primek to je jedno, zda jako prvni promenna bude x nebo y.
V pripade paraboly orientovane podle osy x (ten druhy pripad) bych volila jako prvni - meze pro y - interval na ose y. A pak x = f(y).
Dalsi situace jeste nastane, pokud budeme potrebovat transformovat do polarnich souradnic (oblast je kruh nebo cast kruhu).
To je takovy polopaticky vyklad, matematickou podstatu uz si nejak nevybavuji (pokud jsem ji vubec kdy vedela:-)
Mam nascanovano nekolik kompletne vypocitanych prikladu i s obrazky, tak bych zaslala, pokud bude zajem.
http://mat.fsv.cvut.cz/Sibrava/Vyuka/vic_int.pdf - tady jeste nejake priklady.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Výpočet integrační oblasti u dvojného integrálu (TOTO TÉMA JE VYŘEŠENÉ)