Matematické Fórum

O.o · 05. 12. 2009 22:55

Zdravím,
chtěl poprosit o pomoc, mám tu nějaký příklad s pravděpodobností a nemůžu se tím prokousat (jsem na tohle "levej").

Př:
Jaká je pravděpodobnost, že náhodně zvolené čtyřmístné číslo má:
a) všechny číslice různé
b) právě dvě číslice stejné
c) tři číslice stejné
d) všechny číslice stejné
[Výsledky: a) P=0,504; b) P=0,432; c) P=0,085; d) P=0,001]

Zatím jsem se dostal k řešení u a) a d), ale ne u b) a c).

a) $P(A)=\frac{9 \cdot 9 \cdot 8 \cdot 7}{9 \cdot 10^3}=0,504$
d) $P(B)=\frac{9 \cdot 1 \cdot 1 \cdot 1}{9 \cdot 10^3}=1 \cdot 10^{-3}$

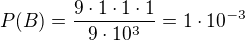
Takto jsem postupoval - jmenovatel: celkem mám 9*10^3 možností; čitatel: příznivých je 9*9*8*7 pro neopakující se číslice a 9*1*1*1 pro stejné číslice (jedno číslo zvolím, další jsou stejná).

Mohl byhc požádat, jestli byste se mi na to někdo nemrknul (i na to a) a d))? Musím říct, že v téhle části (statistika) se ztrácím až nepříjemně moc.

Díky předem za pomoc..

PS: Myslím, že by to mohlo patřit do sekce střední škola..

marnes · 05. 12. 2009 23:07 — Editoval marnes (05. 12. 2009 23:24)

↑ O.o:
a)d) bych řekl OK

b) budu se bavit o čitateli: 9.1.9.8 - ty neobsahují dvě nuly + 9.1.1.8 - ty obsahují dvě nuly

c)9.1.1.9 - ty neobsahují tři nuly + 9.1.1.1 - ty obsahují tři nuly

marnes · 05. 12. 2009 23:34 — Editoval marnes (05. 12. 2009 23:35)

↑ marnes:
opravuju b) tato úvaha: na řádu tisíců 9 a shoda postupně na stovkách, desítkách a jednotkách - vždy 9.8.1, celkem tedy 3. 9.9.8.1 + nyní na řádu tisíců 9, ale shoda bude stovky desítky, nebo stovky jednotky, nebo desítky a jednotky - vždy tedy 9.9.8.1 - celekem 3.9.9.8.1
úplně celkem tedy 6.9.9.8.1 a vychází:-)

marnes · 05. 12. 2009 23:47 — Editoval marnes (05. 12. 2009 23:48)

↑ marnes:
opravuji c)

na řádu tisíců 9 a shoda na stovky a desítky, stovky a jednotky, desítky a jednotky - vždy 9.1.1.9 - celkem 3.9.1.1.9 + na řádů tisíců 9 a shoda na stovkách, desítkách a jednotkách 9- celkem 9.9.1.1
celkem tedy 3.9.1.1.9+81=324 ale nevychází:-(

snad se někdo přidá

O.o · 05. 12. 2009 23:57

↑ marnes:

Ještě jednou ahoj,

u b) jsem doputoval ke stejnému řešení a u c) jsem skončil také u "nevychází" -). Dám tomu ještě pár minut a pokračuji zítra ráno.

Matematické Fórum

#1 05. 12. 2009 22:55

Pravděpodobnost

#2 05. 12. 2009 23:07 — Editoval marnes (05. 12. 2009 23:24)

Re: Pravděpodobnost

#3 05. 12. 2009 23:34 — Editoval marnes (05. 12. 2009 23:35)

Re: Pravděpodobnost

#4 05. 12. 2009 23:47 — Editoval marnes (05. 12. 2009 23:48)

Re: Pravděpodobnost

#5 05. 12. 2009 23:57

Re: Pravděpodobnost

Zápatí