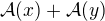Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » linearní zobrazeni (TOTO TÉMA JE VYŘEŠENÉ)
#2 30. 01. 2008 01:24
Re: linearní zobrazeni
No, ja to ted rozepsal tak sahodlouze, nevim, jestli je to moje reseni nejrychlejsi.
Krome aditivity musis overit i homogenitu - jde to zaroven - a to nasledovne - (zobrazeni oznacim po nasem - "A"):
necht mame vektory x=(x1,x2) a y=(y1,y2) a cislo z telesa: napr. "@" :-)
Chceme overit, zdali A(@*x+y)=@*A(x)+A(y)
tedy:
A(@*x+y) = A(@*(x1,x2)+(y1,y2)) = {provedeme nasobeni zavinacem a secteme vektory} = A(@*x1+y1,@*x2+y2) = {provedeme zobrazeni} = (@*x1+y1+2*@x2+2y2, 2*@*x1+2*y1-@*x2-y2) = (@*(x1+2*x2) + (y1+2*y2), @*(2*x1-x2)+(2y1-y2)) = {to je to samy jako} = (@*(x1+2*x2), @*(2*x1-x2)) + ((y1+2*y2),(2y1-y2)) = {a mezitim jeste vytkneme zavinac pred vektor, ale to uz nebudu rozepisovat} = @A(x) + A(y)
Q.E.D.
muhehe, to jsem se vyradil. Nemel uz bych se konecne naucit v nejakym tom TeXu? :-)
Kdyz si to rozepises na papir a zavinac nahradis snesitelnejsi alfou, tak to pochopis :-)
Offline
#6 30. 01. 2008 15:48 — Editoval Tomsus (30. 01. 2008 15:49)
Re: linearní zobrazeni
Vem si treba zobrazeni dany predpisem A(x)=x+1, x je vektor z R^1. Potom A(x) + A(y) = (x+1) + (y+1) = x + y + 2. Na druhou stranu A(x+y) = (x+y)+1. Coz neni samozrejme to same. Trosku obecne se da asi rict, ze linearni zobrazeni muze scitat souradnice vektoru, nasobit je konstantou, brat imaginarni a realne cleny komplexnich cisel a pracovat s nimi, ale nemuze pricitat konstanty.
Offline
#12 30. 01. 2008 18:00
Re: linearní zobrazeni
↑ h4ck3r001: jakmile nejsou ve složkách toho zobrazení lineární kombinace vcházejících vektorů, většinou něco smrdí
Offline
#15 31. 01. 2008 16:21
Re: linearní zobrazeni
příklad: vyřešte soustavu lineárních rovnic. Některým z těchto způsobů - pomocí Cramerova pravidla, maticové rovnice (inverze matic), Jordanova eliminační metoda a zda je splněna Frobeniova věta, řešitelnost či neřešitelnost soustavy, případně počet řešení. Mockrát děkuji.
x_1 - 2X_2 - X_3 + 4x_4 = 9
x_1 - 3x_2 + 5x_3 - 6x_4 = 7
x_1 - X_2 + 2x_3 - x_4 = 2
-x_1 + x_2 + x_3 - 2x_4 = -5
Offline
#16 31. 01. 2008 17:23
Re: linearní zobrazeni
Určete definiční obor funkce a zapište matematické výrazy pomocí editoru rovnic.
\f (x) = \frac(3)(1n(x+2))
\f (x) = \frac(1)(\sqrt sin x -\frac12)
Vypočtěte limity funkcí. Vysvětlete chování funkce v okolí bodu, v němž limitu určujeme.
\lim(x\rightharrow0(\frac1 1-x) - \frac3 1-x^3)
\lim(x\rightharrow0 \frac(3x^2-sin^2x)(2x^2)
V případě, že s tím půjde něco udělat, děkuji za pomoc a za trpělivost. matiku jsem měl naposled SOU. Díky Adis.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » linearní zobrazeni (TOTO TÉMA JE VYŘEŠENÉ)
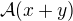 a
a