Matematické Fórum

RobbieMan

Zdravim, mohl by mi nekdo prosim trochu napovedet co s touhle nekonecnou radou, konvergence ci divergence v zavislosti na realnem parametru a
$\sum_\(lnn!/n^a$
zapsane to neni uplne dobre, samozrejme to lomitko znaci zlomek a "lnn!" znaci "ln(n!)"
Dekuji za pomoc, nejak se mi nedari najit srovnavaci protejsek vuci tomu logaritmu s faktorialem.

Olin · 18. 12. 2009 21:41

Zkusil bych použít (viz diskrétka)
$n^{\frac n2} \leq n! \leq n^n$
odtud
$\frac n2 \ln n \leq \ln n! \leq n \ln n$
z čehož už dostáváme dost silnou souvislost s řadou $\sum \frac{n \ln n}{n^a}$ .

RobbieMan · 19. 12. 2009 09:39

diky, to bylo opravdu duvtipne, pak staci pouzit akorat "p-test", ale trochu me trapi to ze, pouzitim tehle rady, potazmo horniho odhadu 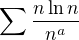$\sum \frac{n \ln n}{n^a}$ se mozna trochu zkresluje vysledek (i kdyz to je spravne podle "demidovichova klíče"), diky za pomoc

Olin · 19. 12. 2009 12:55 — Editoval Olin (19. 12. 2009 13:11)

Tak jsem si našel, co to je ten p-test - ještě by mě zajímalo, jak se přesně zbavíš toho logaritmu? Já jsem tu řadu ještě vlastně neřešil, ale říkal jsem si, že tu novou umlátím Cauchyho kondenzátorem.

A ještě co myslíš tím, že se "zkresluje výsledek"? Samozřejmě, že ta nová řada bude mít jiný součet než ta původní, ovšem vzhledem k tomu, že máme i dolní odhad, můžeme říct, že jedna řada konverguje právě tehdy (a jen tehdy), když konverguje ta druhé, takže pro účely vyšetření konvergence neztratíme nic.

RobbieMan · 19. 12. 2009 17:32

tak sem se neuvazlive unahlil, omylem sem ten logaritmus trochu ignoroval, pak me napadlo seshora ohranicit ten logaritmus odmocninou z n , jenze to vychazi konvergence pro "a" vetsi nez pet polovin, ale ma to bejt vetsi nez 2,

Olin · 19. 12. 2009 17:36 — Editoval Olin (19. 12. 2009 17:49)

Jak jsem říkal, Cauchyho kondensační kritérium je v tomto případě užitečné.

Jen je třeba si rozmyslet, jak je to se splněním jeho předpokladů.

Matematické Fórum

#1 18. 12. 2009 21:15 — Editoval RobbieMan (18. 12. 2009 21:23)

Pomoc s nekonečnou řadou

#2 18. 12. 2009 21:41

Re: Pomoc s nekonečnou řadou

#3 19. 12. 2009 09:39

Re: Pomoc s nekonečnou řadou

#4 19. 12. 2009 12:55 — Editoval Olin (19. 12. 2009 13:11)

Re: Pomoc s nekonečnou řadou

#5 19. 12. 2009 17:32

Re: Pomoc s nekonečnou řadou

#6 19. 12. 2009 17:36 — Editoval Olin (19. 12. 2009 17:49)

Re: Pomoc s nekonečnou řadou

Zápatí