Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » diferencialni rovnice (TOTO TÉMA JE VYŘEŠENÉ)
#2 02. 02. 2008 08:43
Re: diferencialni rovnice
Tak ted nevim jestli mas alespon poneti o tom jak se resi takove diferencialni rovnice. Budu prepokladat ze ano.
Nejprve najdeme fundamentalni system, mame konstantni koeficienty, cili staci najit koreny charakteristickeho polynomu. Ten je jeden a sice cislo 2, tedy fundamentali system je
e^(2x), x*e^(2x)
Nyni hledejme partikularni reseni.
Pouzijeme postup, kteremu se nekdy rika "metoda odhadu". Mame specialni tvar prave strany p(x)e^(ax). Kde p(x) je polynom. V nasem pripade a=2 a p(x) ma stupen nula. Potom existuje q(x) polynom stupne <= p(x), pro ktery plati:
y0 = x^N*q(x)*e^(ax)
kde N je nasobnost korenu "a" charakteristickeho polynomu. Cili pro nas pripad:
y0 = x^2*b*e^(2x) = x^2*e^(2x)
Kde b je konstanta, nebot polynom nulteho stupne je konstanta. Nyni staci dosadit toto y0 za promennou y do puvodni rovnice a spocitat, cemu se rovna b.
Reseni potom vypada takto: 1/2*x^2*e^(2x) + c1*e^(2x) + c2*x*e^(2x) = e^(2x)*(1/2*x^2 + c2*x + c1)
Nothing in the world that's worth having comes easy.
Always do what you are most afraid of.
Offline
#5 02. 02. 2008 15:24
Re: diferencialni rovnice
A nejde to spocitat jeste nejak jinak? protoze tohle mi do hlavy moc nejde, co si tak pamatuju, tak ve skole sme tyhle rovnice upravovali nejak na dy/dx a pak z toho udelali integraly pro x a y, ale tohle je asi jinej typ prikladu a krom toho je tam jeste y'' a to me dost mate
Offline
#6 02. 02. 2008 15:43
Re: diferencialni rovnice
Asi mas na mysli diferencialni rovnice se separovanymi promennymi. Ty se resi tim zpusobem co jsi popsal. To jsou ale velmi specialni typy rovnic a tahle do nich zrovna nepatri (mimo jine proto ze je tam to y'').
Ten tvuj priklad je vylozene typickym prikladem na tu metodu odhadu. Pokud existuje rychlejsi reseni, tak ja ho neznam.
Nothing in the world that's worth having comes easy.
Always do what you are most afraid of.
Offline
#7 02. 02. 2008 16:10
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: diferencialni rovnice
http://mathonline.fme.vutbr.cz/Linearni … fault.aspx
zkus se podivat sem - je to docelo prehledne a v resenych prikladech je i hodne podobny priklad jak mas. Hodne zdaru :-)
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » diferencialni rovnice (TOTO TÉMA JE VYŘEŠENÉ)
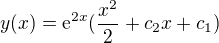 .
.