Matematické Fórum

pzag · 20. 12. 2009 20:26 — Editoval pzag (20. 12. 2009 20:27)

Ahoj, narazil jsem na problém při výpočtu lin. závislosti vektorů a kombinací. Dva vektory jsem vždycky upravoval tak, že jsem řekl, že jeden je k násobek druhého. Vypočetl k ze soustavy a popř. upravil aby to nebylo a = kb ale a-kb = 0. U Tří se mi už vyplatilo udělat matici s nulama na jedné straně a řešin Gaussovou metodou, ale narazil jsem na příklad a nevím. Mám určit zda jsou lin. závislé a určit lineární kombinaci.

a = (-3;0; 2) ; b = (1;1; 1); c = (2;3; 2) ; d = (0;4; 1)

znám výsledek: jsou závislé, a -31b + 17c - 5d = 0
ale nemůžu se dopočítat. Nějak nevím co s tou soustavou, tam mi to vychází na parametr, ale žádný ve výsledku není. Nemoh by to někdo zkusit spočítat.

Oxyd · 20. 12. 2009 20:28 — Editoval Oxyd (20. 12. 2009 21:07)

↑ pzag:

Moc nechápu, co vlastně chceš počítat. Lineární závislost jsi určil, netriviální lineární kombinaci, která dá nulový vektor, jsi též našel, čímž si splnil zadání.

Edit: Už chápu -- k zadání jsi dostal i výsledky, ale nevíš, jak se k tomu dopracovat. Nuže tedy..

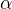Máme dány vektory $a = \begin{pmatrix} -3 \nl 0 \nl 2 \end{pmatrix}$ , $b = \begin{pmatrix} 1 \nl 1 \nl 1 \end{pmatrix}$ , $c = \begin{pmatrix} 2 \nl 3 \nl 2 \end{pmatrix}$ , $d = \begin{pmatrix} 0 \nl 4 \nl 1 \end{pmatrix}$ . Hledáme netriviální řešení rovnice $\alpha a + \beta b + \gamma c + \delta d = \vec{0}$ , pro $\alpha$ , $\beta$ , $\gamma$ , $\delta$ reálná.

Jinými slovy, řešíme soustavu rovnic

$-3 \alpha + \beta + 2 \gamma + 0 \delta = 0$
$0 \alpha + \beta + 3 \gamma + 4 \delta = 0$
$2 \alpha + \beta + 2 \gamma + \delta = 0$

Tak si ji přepišme do matice a aplikujme algoritmus pana Gausse:

$\begin{pmatrix} -3 & 1 & 2 & 0 \nl 0 & 1 & 3 & 4 \nl 2 & 1 & 2 & 1 \end{pmatrix} \sim \begin{pmatrix} -3 & 1 & 2 & 0 \nl 0 & 1 & 3 & 4 \nl 6 & 3 & 6 & 3 \end{pmatrix} \sim \begin{pmatrix} -3 & 1 & 2 & 0 \nl 0 & 1 & 3 & 4 \nl 0 & 5 & 10 & 3 \end{pmatrix} \sim \begin{pmatrix} -3 & 1 & 2 & 0 \nl 0 & 1 & 3 & 4 \nl 0 & 0 & -5 & -17 \end{pmatrix}$

(Pravé strany vynechány, stejně sou všechny nulové.)

Poslední řádka odpovídá rovnici $-5 \gamma -17 \delta = 0$ -- jedno z možných řešení je $\gamma = 17$ , $\delta = -5$ . To samozřejmě není řešení jediné, a tady ses možná zasekl a zavedl parametr -- jak ale řikám, tobě stačí jenom jedno řešení téhle rovnice, takže si můžeš do toho parametru dosadit nějaké konkrétní číslo a pak parametr zahodit.

Když teda víme $\gamma$ a $\delta$ (respektive, zvolili jsme si je, aby nám poslední řádka vycházela), tak když dosadíme příslušné hodnoty do posledních dvou sloupců poslední matice, dostáváme soustavu rovnic:

$-3 \alpha + \beta + 34 = 0$
$\beta + 31 = 0$

Řešením soustavy je $\alpha = 1$ , $\beta = -31$ .

Ovšem tím jsme vyřešili rovnici $\alpha a + \beta b + \gamma c + \delta d = \vec{0}$ -- konkrétně po dosazení vypočítaných koeficientů to je $a - 31 b + 17 c - 5d = \vec{0}$ -- což je to, co máš ve výsledku.

pzag · 20. 12. 2009 22:02

Jo, tak děkuju, k tomu řádku 0 0 -5 -17 jsem došel taky a pak jsem zkončil. Vůbec mě to nenapadlo.

pzag · 20. 12. 2009 22:56

Ještě jsem se chtěl zeptat, jak je to s tím skládáním vektorů do sloupců. Tady je to jasný, řeším tři rovnice o čtyřech neznámých, takže vždycky když budu řešit LZ/LN tak skládat do sloupců, ale vždycky jsem skládal vektory do řádků, třeba když jsem chtěl bázi. Můsím to dělat znovu v řádcích nebo to jde i když to mám takhle?

Oxyd · 20. 12. 2009 23:42 — Editoval Oxyd (20. 12. 2009 23:43)

pzag napsal(a):
Ještě jsem se chtěl zeptat, jak je to s tím skládáním vektorů do sloupců. Tady je to jasný, řeším tři rovnice o čtyřech neznámých, takže vždycky když budu řešit LZ/LN tak skládat do sloupců, ale vždycky jsem skládal vektory do řádků, třeba když jsem chtěl bázi. Můsím to dělat znovu v řádcích nebo to jde i když to mám takhle?

To záleží na tom, co přesně děláš. Tady jsem ty vektory nasázel do sloupečků, protože mi to vyplynulo z té rovnice $\alpha a + \beta b + \gamma c + \delta d = \vec{0}$ -- kdybys to přepsal do řádků, tak z toho dostaneš nějakou matici, která ale vůbec neodpovídá téhle rovnici.

Když naopak hledáš bázi, tak máš dány nějaké vektory a chceš to vyeliminovat na nějakou lineárně nezávislou množinu. Ta Gaussova eliminace pracuje na řádcích, takže když si ty vektory dáš do řádků a eliminuješ, tak ty nenulové řádky ti pak dají lineárně nezávislé vektory, které budou pak ta báze. Když tyhle tři vektory dáš do řádků a eliminuješ to, tak ti vypadne něco jako

$\begin{pmatrix} 1 & 1 & 1 \nl 0 & 0 & 1 \nl 0 & 0 & 0 \nl 0 & 0 & 0 \end{pmatrix}$

(Pokud tam nemám nějakou početní chybu.) To nám v zásadě odpovídá na půlku otázky, „Vektory jsou lineárně závislé“ (jinak by nám tam nevypadly nulové řádky) -- nedává to ovšem tu lineární kombinaci nulového vektoru. Navíc z těhle nových čtyř vektorů nespočítáš tu LK nuly -- sice tyhle čtyři jsou lineárně závislé, a dala by se nula nakombinovat třeba jako jedenkrát poslední řádek, plus nulakrát všechny předchozí, ale to očividně není správná LK pro původní vektory.

Matematické Fórum

#1 20. 12. 2009 20:26 — Editoval pzag (20. 12. 2009 20:27)

Lineárně závislé vektory

#2 20. 12. 2009 20:28 — Editoval Oxyd (20. 12. 2009 21:07)

Re: Lineárně závislé vektory

#3 20. 12. 2009 22:02

Re: Lineárně závislé vektory

#4 20. 12. 2009 22:56

Re: Lineárně závislé vektory

#5 20. 12. 2009 23:42 — Editoval Oxyd (20. 12. 2009 23:43)

Re: Lineárně závislé vektory

pzag napsal(a):

Zápatí