Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 21. 12. 2009 12:38
- MichaelaM.
- Zelenáč
- Příspěvky: 12
- Reputace: 0
Derivace funkce
Ahoj. Chtěla jsem Vás poprosit o pomoc s tímdle příkladem. Vůbec nevím co s tím. Mohl byste mi někdo napsat co a jak s tím? A hlavně proč? Děkuju moc.
f:y=cos x^6
Offline
#4 21. 12. 2009 12:59
- MichaelaM.
- Zelenáč
- Příspěvky: 12
- Reputace: 0
Re: Derivace funkce
Zkusila jsem to podle toho vzorečku a vyšlo mi:
-6sinx*cos^5x
Je to správně?
Offline
#5 21. 12. 2009 13:30
#7 21. 12. 2009 13:48 — Editoval Cheop (21. 12. 2009 13:50)
#8 21. 12. 2009 14:20
- MichaelaM.
- Zelenáč
- Příspěvky: 12
- Reputace: 0
Re: Derivace funkce
Tak teď to teda nechápu...jak je teda derivace té původní funkce?
Offline
#9 21. 12. 2009 14:21
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: Derivace funkce
↑ MichaelaM.:
Tys nám neřekla, která funkce je původní.
Offline
#10 21. 12. 2009 14:26
- MichaelaM.
- Zelenáč
- Příspěvky: 12
- Reputace: 0
Re: Derivace funkce
No todle je funkce, kterou potřebuji zderivovat f:y=cos x^6. Takže je snad původní ne?
Offline
#11 21. 12. 2009 14:29
Re: Derivace funkce
↑ MichaelaM.:
To určitě je, ale je zapsaná nejednoznačně, viz hned první příspěvek od halogana. Je to 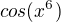 nebo
nebo  ?
?
Offline
#13 21. 12. 2009 14:36 — Editoval LukasM (21. 12. 2009 14:38)
Re: Derivace funkce
↑ MichaelaM.:
Jestli je to 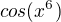 , tak máš tu derivaci špatně.
, tak máš tu derivaci špatně.
Jinak doporučuju na tyhle kontroly Wolfram Alpha.
Edit: napsal jsem původně "správně", snad to nikdo nestihl přečíst.
Offline
#14 21. 12. 2009 14:39
- MichaelaM.
- Zelenáč
- Příspěvky: 12
- Reputace: 0
Re: Derivace funkce
Aha tak díky moc...určitě mi to pomůže...Ještě se chci zeptat co znamená při řešení lineárních rovnic, když je bazické řešení degenerované...
Offline
#16 21. 12. 2009 14:56
- MichaelaM.
- Zelenáč
- Příspěvky: 12
- Reputace: 0
Re: Derivace funkce
Jasně dík moc..a jak je to s tim degenerovanym řešením nevíte?
Offline
#17 21. 12. 2009 15:27
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Derivace funkce
↑ MichaelaM.:
Zdravím,
zřejmě řešíš úlohu lineárního programování - degenerované řešení soustavy lineárních rovnic obsahuje alespoň jednu 0. Podrobně, například zde - oblibené vydavatelství VŠCHT. (kapitola2.3). Je to ten problém, který řešiš?
Offline
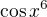 nebo
nebo 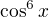 ?
?
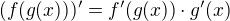

 je to takhle...
je to takhle...