Matematické Fórum

Petuhik · 17. 12. 2009 22:07

ahoj, chtěla bych se zeptat, zda-li by byl někdo tak ochotný a pomohl mi s příklady, která mám mít do školy. Jednalo by se o nekonečné řady a diferenciální rovnice :-(

Doxxik · 17. 12. 2009 22:10

určitě se tu nějaká dobrá duše najde ;) .. zkus je sem přepsat (nebo sem dej alespoň link na ně) + napiš, s čím bys potřebovala pomoci..

Petuhik

↑ Doxxik:

děkuji moc, tohle mě opravdu potěšilo. Totálně se ztrácím ve slovních úlohách. Mám 2, se kterými si totálně nevím rady. Vím, že se to bude řešit nějak pomocí rovnic, ale nevím vůbec jak:-(, protože tam pro mě chybí prostě dost číselných údajů, hlavně teda v té první...

1. Pěstujeme bakterie, které se množí tak, že rychlost růstu jejich populace je přímo úměrná stávajícímu počtu. Po jedné hodině šlechtění jsme zaznamenali nárůst jejich počtu o 1/2. Za jak dlouho jich bude trojnásobek?

2. V nádrži o objemu 500 litrů je 200 litrů čisté vody. Do nádrže přitéká slaná voda, obsahujícící 1/4 kg soli v jednom litru, rychlostí 3 litry za minutu. Z druhého konce odtéka smíchaný roztok rychlostí 2 litry za minutu.
a) Vyjádřete množství soli (kg) v nádrži jako funkci času (min).
b) Kolik soli je v nádrži v okamžiku, kdy je plná?

Prosím pomozte:-(

Doxxik · 18. 12. 2009 14:36 — Editoval Doxxik (18. 12. 2009 14:46)

zde jsou mé úvahy o řešení:

2)
a - označíme si množství soli X v nádrži (v kg), t = čas (v minutách)
protože je na začátku 0kg soli v nádrži, bude X_0 = 0
dále musíme zjistit, jak rychle přibývá sůl. Víme, že z prvního přívodu přiteče za 1 minutu 3 litry a z druhého 2 litry (celkem tedy 5 litrů roztoku za minutu). Víme rovněž, že jeden litr roztoku obsahuje 1/4kg soli. Od tud tedy za 1 minutu přibude v nádrži 5/4kg soli. Vyjádříme si tedy příbytek soli (deltaX) za změnu času (delta t):
deltaX = (delta t) * 5/4.

obecně bych si X (aktuální množství) vyjádřil jako X_0 (počáteční) + deltaX (příbytek).

Z výše uvedených poznatků můžeme upravovat:
X = X_0 + deltaX = 0 + deltaX
X = deltaX
X = (delta t) * 5/4

dále musíme omezit t. Protože se nádrž bude plnit nejdéle 1 hodinu = 60minut (viz níže), musí t náležet intervalu <0;60>

b - zbývá naplnit 300litrů. protože každou minutu přiteče celkem 5 litrů (2+3), víme, že se naplní nádrž za 60minut. A pak stačí spočítat, kolik soli vyprodukují jednotlivé nádrže za tu jednu hodinu->
1. přívod - 1/4 za minutu a litr -> 60/4 = 15kg za hodinu a litr -> 3*15 = 45kg za hodinu a tři litry
2. přívod - (předpokládám, že smíchaný bez dalších indícií znamená opět 1/4 za minutu a litr) -> 1/4 za minutu a litr -> 15 za hodinu a litr -> 30 za hodinu a dva litry

celkem tedy 30+45 = 75kg
---
pozn.: pracuji na zbytku

Doxxik · 18. 12. 2009 14:57

1) protože se vždy rozrostou v závislosti na jejich aktuálním počtu, myslím, že můžeme prohlásit, že platí:
a_(n+1) = a_n * x (kde x je jakýsi růstový koeficient), což evokuje geom. posloupnost.

ze zadání je zřejmé, že x musí být závislé na čase t (tedy třeba x = y (koeficient příbytku za jednu jednotku času) * t). rovnice by mohla vypadat tedy: a_(n+1) = a_n * y * t

je zadáno, že pokud se při měření zjistilo, že příbytek byl 1/2 aktuálního počtu, tedy a_(n+1) = 3/2 * a_n.
Z čehož je patrné, že y*t = 3/2 kde t je 60 minut, tedy zskáváme jednu rovnici:

y * 60 = 3/2 -> y = 3/(3*20*2) = 1/40

ptáme se, za jak dlouho bude příbytek roven 1/3, tedy i y*t = 1/3
y jsme si výše spočítali, neznámá je pouze čas t v minutách.. stačí dosadit a dopočítat..

zdenek1

↑ Petuhik:
1. Počet bakterií $N$
$\frac{dN}{dt}=kN$ podle zadání
$\frac{dN}N=kdt\ \Rightarrow\ \int\frac{dN}N=\int kdt\ \Rightarrow\ \ln N=kt+C$
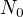V čase $t=0$ je $N_0$ batterií, proto $C=\ln N_0$
Po úpravách $N=N_0 e^{kt}$
Z $N(1)=\frac32 N_0$ zjitíme $k$ $\frac32N_0=N_0e^k\ \Rightarrow\ e^k=\frac32$ , takže $N=N_0\left(\frac32\right)^t$

V nějakém čase $t$ je $N=3N_0=N_0\left(\frac32\right)^t$

$t=\frac{\ln3}{\ln3-\ln2}$

Petuhik

↑ Doxxik:

tak tohle by mě opravdu nenapadlo. Takže ten výsledek u příkladu č.1 je: t = 40/3. A je to super pochopitelné. vážně moc děkuju. Ale ten postup od Zdenka 1 nějak moc nechápu, i když to v podstatě vypadá stejně:-)

A ten druhý příklad my přijde malinko zmatený. Do nádrže má jedním přívodem voda PŘÍTÉKAT a druhým ODTÉKAT. jak je tedy možné, že počítáš s 5 litry:-(

Doxxik · 18. 12. 2009 22:50

moc se omlouvám, že jsem udělal zmatky.. (jsou to zmatky z nepozornosti, o to je to horší..). Toho "odtéká" jsem si vážně nevšiml..

Petuhik · 19. 12. 2009 10:21

↑ Doxxik:

to vůbec nevadí. mohla bych tě teda poprosit o nový výpočet?vím že sem otravná, ale ty si moc hodný. Děkuju...

halogan · 19. 12. 2009 10:53

No, spíš se mi zamlouvá Zdeňkův postup. Ve finále stačí spočítat
$(3/2)^x = 3$

Což zlogaritmuješ a použiješ tabulkové hodnoty logaritmů.

Až budu u počítače, tak se rád víc rozepíšu.

LukasM · 19. 12. 2009 11:06 — Editoval LukasM (19. 12. 2009 11:13)

↑ Petuhik:
Ahoj. Taky se přidám, snad nenapíšu nějaký nesmysl. Ten postup od Zdeňka bych tak rychle nezatracoval.

Postup od Doxxika je sice dobře vymyšlený, akorát mně dlouho mátlo to indexování členů posloupnosti neurčitými čísly s n-ky. Nakonec jsem ale pochopil, že nechává bakterie množit každou minutu. Problém ale je, že bakterie nejsou minutu v klidu, a potom se rozmnoží, ale množí se stále. Navíc je špatně dosazení na konci - otázka zněla kdy je jich trojnásobek, ne 1/3. Pokud dosadíme správně, vyjde 120 minut (což je o trochu uvěřitelnější než 40/3=11 minut - a to odporuje zadání).
Jinak ta otázka kdy jich bude třetina už podle zadání nemůže mít odpověď (resp. musí vyjít záporné číslo). Pokud vyjde 40/3, je někde něco špatně s metodou výpočtu.

Zdeňkův výpočet je principiálně správně, a dává 2,7 h = 162minut.

Snad jsem nic nepřehlédl.

Edit: Jsem pomalej. Ještě doplním, že Doxxikův postup se nedá vylepšit množením třeba po 1 sekundě, a to prostě proto, že ta naše kalibrační podmínka je přírůstek bakterií za celou hodinu - takže vypočítané y se při výpočtu pro jednu sekundu "nezlepší".

Petuhik

↑ LukasM:

aha. tak tomu už teda moc nerozumím. Mohl by mi prosím teda někdo poslat celé správné postupy?děkuji mnohokrát:-(

halogan · 22. 12. 2009 18:04

1) Co my víme? Že za určitou jednotku času (tady to je jedna hodina) se nám zvýšil jejich počet o 50 %, tedy nárůst o 1/2.

$\text{novy pocet} = \text{stary pocet} \cdot \frac{3}{2} = \text{stary pocet} \cdot (1 + \frac 12)$

Je tohle jasné? Budu teď nový počet značit NP a starý počet SP.

Po jedné jednotce času bude platit $\text{NP} = \text{SP} \cdot \frac 32$ , po dvou jednotkách bude $\text{NP}_2 = \text{SP} \cdot \frac 32 \cdot \frac 32$ . Po $n$ jednotkách času bude platit $\text{NP}_3 = \text{SP} \cdot $\frac 32$^n$ . Jasné?

Nám jde o to, aby se starý počet (SP) ztrojnásobil. Tedy abychom násobili tuto hodnotu trojkou. A čím to násobíme? Výrazem (3/2)^n. Řešíme tedy:

$$\frac 32$^n = 3$

Zlogaritmujeme a už to máme. $n$ je počet hodin.

Petuhik

↑ halogan:

no, tomu zatím rozumím,ale právě mě zatím nejde na mozek ten starý počet - jako kolik jich bylo na začátku. Jinak všemu rozumím.

halogan · 22. 12. 2009 19:04

Jo, starý počet je původní počet. Ten nás vlastně nezajímá, jen aby to bylo k pochopení.

Petuhik · 22. 12. 2009 19:06

↑ halogan:

hm.....tak jooo. a ještě jeden dotaz, jak zlogaritmuju ten poslední výraz (3/2)^n = 3???

Olin · 22. 12. 2009 19:07 — Editoval Olin (22. 12. 2009 19:08)

Podle vzorce $\log (a^b) = b \cdot \log a$ .

Petuhik · 22. 12. 2009 19:30

↑ halogan:

je možný,že by mi vyšlo tohle:

log (3/2) ^n = 3

n* log (3/2) = 3

0,176 n = 3

n = 17,045 ??????????

halogan · 22. 12. 2009 20:07

Takže jsi zlogaritmovala levou stranu a pravou jsi nechala jen tak být?

Petuhik · 22. 12. 2009 20:12

↑ halogan:

a takhle už by to mohlo být. že????

log (3/2) ^n = log 3

n* log (3/2) = log 3

0,176 n = 0,477

n = 2,710 ??????????

halogan · 22. 12. 2009 20:20

1) Uber pár otazníků. Nebo hodně otazníků.

2) 2.7 a 17 je DOST velký rozdíl. Příště se zamysli nad tim příkladem a uvidíš, že 17 je blbost.

3) Nezaokrouhluj, výsledky dávej v logaritmech.

4) Postup jsi tu měla napsaný asi 3x a nezeptala ses na podrobnosti, jen jsi chtěla další postup.

5) Hezké svátky přeji.

Petuhik

↑ halogan:

mnohokrát ti děkuju. Tobě taky hezké svátky.

Matematické Fórum

#1 17. 12. 2009 22:07

prosba o pomoc

#2 17. 12. 2009 22:10

Re: prosba o pomoc

#3 18. 12. 2009 14:19 — Editoval Petuhik (18. 12. 2009 14:20)

Re: prosba o pomoc

#4 18. 12. 2009 14:36 — Editoval Doxxik (18. 12. 2009 14:46)

Re: prosba o pomoc

#5 18. 12. 2009 14:57

Re: prosba o pomoc

#6 18. 12. 2009 15:04 — Editoval zdenek1 (18. 12. 2009 21:54)

Re: prosba o pomoc

#7 18. 12. 2009 21:43 — Editoval Petuhik (18. 12. 2009 21:52)

Re: prosba o pomoc

#8 18. 12. 2009 22:50

Re: prosba o pomoc

#9 19. 12. 2009 10:21

Re: prosba o pomoc

#10 19. 12. 2009 10:53

Re: prosba o pomoc

#11 19. 12. 2009 11:06 — Editoval LukasM (19. 12. 2009 11:13)

Re: prosba o pomoc

#12 20. 12. 2009 13:19 — Editoval Petuhik (20. 12. 2009 13:20)

Re: prosba o pomoc

#13 22. 12. 2009 18:04

Re: prosba o pomoc

#14 22. 12. 2009 18:18 — Editoval Petuhik (22. 12. 2009 18:28)

Re: prosba o pomoc

#15 22. 12. 2009 19:04

Re: prosba o pomoc

#16 22. 12. 2009 19:06

Re: prosba o pomoc

#17 22. 12. 2009 19:07 — Editoval Olin (22. 12. 2009 19:08)

Re: prosba o pomoc

#18 22. 12. 2009 19:30

Re: prosba o pomoc

#19 22. 12. 2009 20:07

Re: prosba o pomoc

#20 22. 12. 2009 20:12

Re: prosba o pomoc

#21 22. 12. 2009 20:20

Re: prosba o pomoc

#22 22. 12. 2009 20:33 — Editoval Petuhik (22. 12. 2009 20:34)

Re: prosba o pomoc

Zápatí