Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 24. 12. 2009 22:10 — Editoval halogan (24. 12. 2009 22:10)
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: maturita
18.
Upravíme na 
Teď plánujeme udělat neekvivalentní úpravu, tak se podíváme, co máme na obou stranách. Na intervalu (3pí, 4pí) máme určitě záporný sinus, chceme tedy i zápornou pravou stranu. Násobíme -\sqrt{3} něčím a to něco tím pádem musí být kladné. Můžeme se tedy omezit na (7/2 pí, 4pí), tam je kosínus kladný.
No a to už je snadné.
02. jablko + jablko = 2 jablka
---
Jasné oboje?
Offline
#3 24. 12. 2009 22:19
Re: maturita
↑ halogan:
ked tam nasobis mocninou nemas mat -sin na druhu x?
a preco 7/2? nie 7/4?
Offline
#4 24. 12. 2009 23:35
#5 25. 12. 2009 00:32
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: maturita
halogan napsal(a):
Teď plánujeme udělat neekvivalentní úpravu
když už plánujeme neekvivalentní, tak bych levou a pravou stranu podělila 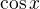 (s případnou poznámkou o nenulovosti, ale ta snad ani nehrozí). Může bý?
(s případnou poznámkou o nenulovosti, ale ta snad ani nehrozí). Může bý?
Pozdrav :-)
Offline
#7 25. 12. 2009 11:53
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: maturita
postup kolegy ↑ halogan: je v pořádku, uvažuje neekvivalentní úpravu "Umocnění levé a pravé strany na druhou", případně okomentuje své úvahy ohledně nalezení příslušného kořene ve stanoveném intervalu.
Můj návrh je podělit (podmínka, že je nenulový, to platí) levou a pravou stranu rovnice
(podmínka, že je nenulový, to platí) levou a pravou stranu rovnice  a vyřešit vzniklou rovnici
a vyřešit vzniklou rovnici  , z periodického zápisu kořenů vyběru ten, která patří do určeného intervalu. Může být?
, z periodického zápisu kořenů vyběru ten, která patří do určeného intervalu. Může být?
Offline
#10 25. 12. 2009 12:52
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: maturita
↑ alikishax:
Rovnice
má v reálných číslech nekonečně mnoho řešení. Když je najdeš, stačí pak vybrat to, které leží v intervalu  .
.
↑ halogan:
Mluvíš o neekvivalentní úpravě, ale nakonec jsi žádnou neprovedl. Na intervalu, na který ses omezil je umocnění ekvivalentní úpravou. Pro  platí
platí .
.
Offline
 , můžeš si i
, můžeš si i  upravit na
upravit na 