Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 25. 12. 2009 16:35
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Geometricka postupnost
↑ alikishax: zapiši jednotlivé členy vzorcem přes 1. člen a_1, q. Vytvořím poměry dle zadání a uvídím jeden "hezký" vztah, který se použije pro odpověď. Dá se všechno zapsat i pro a_5, q - možná bude ještě hezčí vztah, nezkoušela jsem, dej vědet, co bylo hezčí. Děkuji.
Offline
#4 25. 12. 2009 16:38
Re: Geometricka postupnost
↑ alikishax:
No vyuzijeme, ze z vlastnosti geometrickej postupnosti vyplyva: 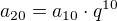 a zaroven zo zadania:
a zaroven zo zadania: 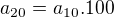 , teda
, teda 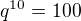 .
.
My chceme vypocitat vlastne hodnotu podielu 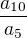 , ale uz vieme, ze
, ale uz vieme, ze 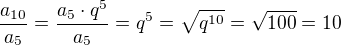 :)
:)
Offline
