Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 07. 12. 2009 19:43
metody řešení
ahoj, chtěla bych poprosit o pomoc s tímto příkladem. Vím, že se ta přímka dosadí do té rovnice kružnice, vyjde kvadaratická rovnice s parametrem, ale nevím co dál s tím.Děkuji moc za pomoc.
V závislosti na parametru a ϵ R vyjádřete průsečíky přímky y = a(x+1) s kružnicí x na 2+y na 2 = 1 a dokažte, že tyto mají racionální souřadnice právě tehdy, když a ϵ Q.
Offline
- (téma jako vyřešené označil(a) jelena)
#3 13. 12. 2009 12:24
Re: metody řešení
ahoj, potřebovala bych pomoct s příkladem: V jisté speciální laboratoři smíme používat pouze laboratnorní váhy o nosnosti 1056 g, 7 závaží o hmotnosi 105 g, 5 závaí o hmotnosti 119g a 4 závaží o hmotnosti 161 g.Určete všechny způsoby, jak odvážit 84 g jisté látky (abychom nepolámali váhu). Která předchozích možností je nejméně energeticky náročná?
Mám pocit, že by se to nějak mohlo pokládat do rovnice, ale nenapá mě právě jak:-(
Offline
#4 13. 12. 2009 20:23
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: metody řešení
↑ Petuhik:
Zdravím, na toto je nějaký standardní postup, který si nemohu vybavit - spojeno se společnými děliteli a násobky:
84, 42 (rozdíl závaží 161-119=42), 14 (rozdíl závaží 119-105=14), 56 (rozdíl závaží 161-105=56)
Například:
na jednu mísku dám 2*161, na druhou 2*119+dovážím 84g, zápis přes děliteli je:
2(161-119)=84
2(161-119)=2*42
nebo 6(119-105)=6*14 což je nemožné - nemáme 6 závaží 119 atd.
Zkus si to takto rozepsat a vyloučit nepovolené možnosti (maximální hmotnost na mísce a počet závaží).
Ale systematický název postupu si nemohu vybavit, snad někdo z kolegů.
Offline
#5 14. 12. 2009 20:23
Re: metody řešení
↑ jelena:
tak jsem to nakonec zkusilla pomocí modul, ale zasekla sem se tam:-(
rovnice: 105x+119y+161z=84
1. zbavení y a z - pomocí modulu 7 - NSD (119,161)=7
- musí platit:105x = 54 (mod 7) » 105x=105 (mod 7) » x = 1 (mod 7) » to znamená, že x = 1+7k pro nějaká celé číslo k.
2.dosadím do rovnice ze zadání: 105(1+7k)+119y+161z=84
150+735k+119y+161z = 84 /:7 a upravím
17y+23z=-105k-3
- odteď považuji k za parametr a zkusme vyjádřit neznámou y.
3. zbavení z - pomocí modulu 5. (23:5=4,6)
- musí platit: 17y=-105k-3 (mod 5)
-----A tady jsem se zasekla:-(nevím, jak mám vypočítat modul 5 s tím parametrem : 17y=-105k-3 :-( ..Prosím o pomoc
Offline
#6 15. 12. 2009 00:24
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: metody řešení
↑ Petuhik:
Zdravím,
bohužel moje představivost nesahá dál, než je úprava 105x+119y+161z=84 (dělením 7) na tvar: 15x+17y+23z=12 a dál už jen vím, že je to nějaký standard na řešení v celých čislech (mince, vahy, kanistry apod.)
Nepochybuji, že kolegové to určitě vyřeší, děkuji :-)
Offline
#7 15. 12. 2009 01:13
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: metody řešení
↑ jelena:Abych mohl pozdravit a poslat písníčku, tak s tím trochu pohnu ...
Rovnice
15x+17y+23z=12
je celkem standardní diofantickou rovnicí. Modulo 15 máme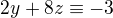 , po vynásobení 8
, po vynásobení 8
takže 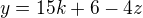 .
.
x+17k-3z=-6
Další úpravy dělat nemusíme, pro libovolné z a k nám vyjde x=3z-17k-6
Máme řešení ve tvaru
(3z-17k-6,15k+6-4z,z). Každá z těchto složek musí být v absolutní hodnotě menší než příslušný počet závaží, což nám dává jistá omezení.
Můžeme si tato omezení vyznačit na čtverečkovaném papíře
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#8 15. 12. 2009 01:23
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: metody řešení
↑ Kondr:
děkuji :-)
------------
a dobře vím, že na mně je dovest náklad do přístavu ... (cíl 5 stran je splněn, snad)
Offline
#10 01. 01. 2010 23:22
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: metody řešení
↑ Petuhik:
Zdravím,
v jakém smyslu je použito zájmeno neurčité "nějaké"? Seznam pojmů pojmenovaných po Leonhardu Eulerovi. Děkuji.
Offline
#12 02. 01. 2010 01:54
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: metody řešení
↑ Petuhik:
Doufám, že máš na mysli: http://en.wikipedia.org/wiki/Euler%E2%8 … at_theorem - je to tak?
Offline
#13 02. 01. 2010 03:27
Re: metody řešení
↑ jelena:
ahoj, jj tohle sem měla na mysli. Už sem to našla. Děkuju. Chtěla bych se zeptat ještě na jednu věc. Existuje nějakej postup,jak z obecnýho čtyřúhleníku sestavit čtverec?? jako rozstříháním????já sem si to rozstříhala na trojúhelníky, ale prostě mi to nejde sestavit.
Offline
#14 02. 01. 2010 17:12
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: metody řešení
↑ Petuhik: Počet odpovědí nezávisí na počtu otazníků :) Pomůže odkaz? http://www.cut-the-knot.org/do_you_know/Bolyai.shtml
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#15 17. 02. 2010 17:08
- kralovnicka
- Příspěvky: 122
- Reputace: 0
Re: metody řešení
↑ Kondr:
mohl bys mi prosim rict, jak si vzal to x+17k-3z=-6?
Offline
#16 17. 02. 2010 17:37
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: metody řešení
↑ kralovnicka: Za y jsem dosadil do původní rovnice a vydělil 15.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
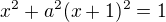
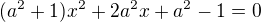 ,
, 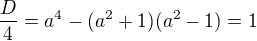
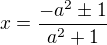
 ,
, 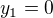
 ,
,