Matematické Fórum

Olin · 03. 01. 2010 16:22

Zdravím,

problém zní:
Nechť $f:[0, 1] \to \mathbb{R}$ je prostá a $f([0, 1]) = [0, 1]$ . Je funkce $f$ spojitá alespoň v jednom bodě $x \in [0, 1]$ ?

Ta otázka je formulována tak, že bych si z ní spíš tipl, že taková funkce musí mít vždy alespoň jeden bod spojitosti… Ale přece jen:

$f(x) = \begin{cases} \frac 12 & \text{pro } x = 0\nl 1 & \text{pro } x = \frac 12\nl 1-x & \text{pro } x \in ([0, 1] \cap \mathbb{Q}) \setminus \{0, \frac 12 \}\nl x & \text{pro } x \in [0, 1] \setminus \mathbb{Q} \end{cases}$

Tato funkce dle mého názoru má limitu pouze v 1/2, ale je 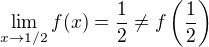$\lim_{x \to 1/2} f(x) = \frac 12 \neq f$ \frac 12 $$ , takže funkce není spojitá nikde. Nebo jsem někde něco přehlédl?

Díky za jakékoliv připomínky a komentáře!