Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 05. 01. 2010 14:18
delitelnost
prosim o pomoc
dokazte.
1, Jestliže a´b|b´a, pak a|b. (znaceni a´b znamena a umocneno na b)
2, Jestliže a|b a b|a, co můžete říci o a a b? Svoji odpověď zdůvodněte.
3, Kolik je 19 na 50000 modulo 33
4, PokudNSD(a,b)=NSD(a,c)=NSD(b,c)=1, platí pak NSD(a,b,c)=1
Offline
- (téma jako vyřešené označil(a) musixx)
#2 05. 01. 2010 14:39
#3 05. 01. 2010 15:02 — Editoval musixx (05. 01. 2010 15:07)
Re: delitelnost
↑ Matik: To první tvrzení není obecně pravda. Je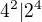 
, ale přitom 
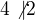. Třetí závisí trochu na tom, jestli znáš Eulerovu větu z teorie čísel (dá se tak ušetřit trochu násobení). No a dvojka a čtverka jsou opravdu snadné, dvojka snad přímo přes definici dělitelnosti, čtverka možná nepřímo...
Offline
#4 06. 01. 2010 17:10
Re: delitelnost
↑ musixx:
a slo by to treti nejak nastinit, nasle jsem jisty postup, avsak u tohoto mi to moc neslo.
spočtěte 17 na 100000 modulo 35.
Modulo 5: 17 na 100000 = 2 na 100000 =2 na 4*250000=1
Modulo 7: 17 na 100000 = 3 na 100000 =3 na 6*16666+4=3 na 4=4
diks
Offline
#5 06. 01. 2010 17:31 — Editoval musixx (06. 01. 2010 17:32)
Re: delitelnost
↑ Matik: Tak analogicky k tomu, co znáš... Náš modul je 33, tedy rozloženo na prvočísla 3 * 11. Podívejme se tedy na číslo 19^50000 pomocí těchto modulů. Základní jednoduché pravidlo je částečné umocňování a snižování základu mocniny pomocí modulu.
modulo 3: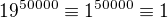 
modulo 11: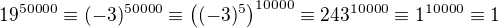 
Teď přijde tzv. Čínská zbytková věta, neboli zjednodušeně když dává číslo zbytek jedna po dělení 3 a 11, tak dává zbytek jedna také po dělení 33, neboli 19 na 50000 modulo 33 je jedna.
Poznámka: U toho modulu 11 jsem měl "štěstí". Také jsem mohl postupovat mnohem pomaleji třeba tudy: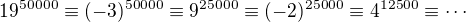
. Ke správnému výsledku bych se ale i tak dostal.
Poznámka2: Udělal jsem to takto "otrocky", protože na Eulerovu větu ses nějak netvářil...
Offline