Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
Téma zavřeno
- Hlavní strana
- » Zajímavé úlohy z pravděpodobnosti a statistiky
- » Statistika (TOTO TÉMA JE VYŘEŠENÉ)
#1 27. 12. 2009 11:43
Statistika
Ahojky, prosím o radu..máme za úkol příklad ze statistiky který se skládá z 6 bodů. Úplně v tom plavu a do konce roku to máme odevzdat :( prosím o pomoc...
Tady je zadání:
1) Pro statistický znak „Plat“ vypočtěte průměr, modus, medián, výběrový rozptyl, výběrovou směrodatnou odchylku, šikmost a špičatost. Poslední dva ukazatele interpretujte. (3 body).
2) Pro statistický znak „Věk“ testujte na pětiprocentní hladině významnosti hypotézu, že průměrný věk v populaci je 34 let. Uveďte hodnotu testového kritéria, kritickou hodnotu a závěr testu („průměrný věk je / není 34 let“). (3 body).
3) Pomocí dvouvýběrového t-testu se stejnými rozptyly zjistěte,zda v Ostravě a v Praze jsou platy v průměru stejné. Uveďte testové kritérium, kritickou hodnotu a závěr testu („plat je/není v průměru stejný“). (3 body).
4) Vypočtěte korelaci mezi věkem a počtem dětí. Koeficient otestujte na významnost (6 bodů).
5) Nalezněte regresní přímku vyjadřující závislost platu na počtu let strávených v práci. Kvalitu modelu zhodnoťte pomocí koeficientu determinace a pro první bod na přímce (bod pro nejmenší x) spočtěte reziduum. (8 bodů).
6) Chí-kvadrát testem zjistěte, zda existuje závislost mezi počtem dětí a místem bydliště. Uveďte hodnotu testového kritéria, kritickou hodnotu a závěr testu. (7 bodů).
Všechny testy se provádějí na pětiprocentní hladině významnosti.
Tady je tabulka z které čerpat:
Věk,Vzdělání,Plat(v tis.),Rodinný stav,Počet dětí,Bydliště ,Počet let v práci
Poznámky
Vzdělání základní 1
střední 2
21 2 13 1 0 1 2 vysokoškolské 3
35 3 20 1 1 2 4
35 2 15 1 1 1 3
32 3 18 1 1 2 2 Rodinný stav
46 3 21 2 1 2 6
53 2 15 2 1 2 10 Svobodný/á 1
57 2 14 1 2 2 10 Ženatý/Vdaná 2
54 2 13 2 1 3 12
57 3 16 2 1 4 12
58 3 15 2 2 2 7 Bydliště Ostrava 1
43 2 16 1 2 2 13 Praha 2
67 3 17 2 2 2 13 Brno 3
45 2 14 2 1 1 2 Plzeň 4
18 2 13 2 0 1 2
43 1 10 1 1 1 23
42 2 13 2 1 2 12
56 2 15 1 2 2 0
45 3 22 2 1 2 1
24 3 25 2 2 3 5
45 3 24 2 1 3 4
34 3 23 2 2 3 3
45 3 22 2 1 2 4
23 3 18 2 2 3 5
45 3 16 1 1 4 6
56 2 15 2 2 1 6
34 2 16 1 1 1 5
32 2 16 1 0 1 3
36 2 14 1 0 3 4
32 3 17 1 0 2 5
45 3 25 2 1 2 12
46 2 17 1 1 2 14
43 2 16 2 0 1 15
47 2 18 2 1 2 16
48 3 21 1 1 1 14
44 2 22 2 1 2 15
41 1 11 2 0 1 13
40 1 10 1 0 1 15
25 1 10 2 0 1 2
24 2 15 2 0 1 2
25 3 16 2 0 2 2
26 2 18 2 0 2 2
27 3 16 1 1 2 1
24 3 18 2 0 2 2
24 2 15 2 0 3 3
Offline
- (téma jako vyřešené označil(a) byk7)
#2 27. 12. 2009 15:04
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Statistika
↑ monex:
Zdravím,
"Čím je tvůj problém zajímavý, že jej píšeš do sekce se zajímavými úlohami." (c)
Například tím, že můžeme uvažovat, čím je zajimavý. Proto moje doplňující otázky:
1) máš EXCEL s doinstalovaným nástrojem "Analýza dat"?
2) jaký teoretický materiál k problému jsi prostudoval(a)? - prosím odkaz.
3) jak (dle tvé představy) má vypadat pomoc v případě takové formulace problému?
Děkuji.
Offline
#3 08. 01. 2010 16:55
Re: Statistika
Zdravím kolegové,
mám tu jeden problém, který zřejmě pro většinu z vás bude banální, nikoliv však pro mě.
Znění zní:
"Následující hodnoty představují úrokové sazby, které byly platné pro určitý typ terminovaných vkladů v ŽIVNOSTENSKÉ BANCE za posledních pět let.
6,2%
4,1%
3,8%
4,4%
3,1%
Určete:
a) Průměrný úrok pro tento typ termínovaných vkladů v této bance za posledních pět let.
b) Za kolik let se vklad zvýší o 30%, budeme-li uvažovat průměrný úrok?"
a) jsem vypočítal pomocí geometrického průměru, jelikož se jedná o koeficienty = 4,2% (je to správně?)
b) netuším, prosím o "nakupnutí"
Děkuji za ochotu.
V matematice věcem neporozumíte — jen si na ně zvyknete.
Offline
#4 08. 01. 2010 17:56 — Editoval jelena (08. 01. 2010 18:42)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Statistika
↑ tommy:
Zdravím,
a) řekla bych, že počítat to přes geometrický průměr není vhodné - ten se používá, když hodnotíme například koeficient růstu vkladů oproti předchozímu období. V případě úroku údaj 6,2 % řekne pouze, že k uspořené částce na účtě je potřeba přidat částku vzniklou z uročení. Můžeš se podívat do materiálů a případně to ještě prodiskutovat. Volila bych aritmetický průměr.
b) až budeš mít průměrný úrok, tak se použije vzorců z využití geometrické posloupnosti pro finanční matematiku. Počáteční vklad  hodnota pro 5 letech (po nárůstu o 30 %) je
hodnota pro 5 letech (po nárůstu o 30 %) je 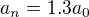 , počítáme n - počet let. Pak už jen vzorce, zřejmě bez zdanění, v zadání není zdanění uvedeno.
, počítáme n - počet let. Pak už jen vzorce, zřejmě bez zdanění, v zadání není zdanění uvedeno.
Toto téma je jinak již vyřešeno, vkládat nový dotaz do vyřešeného tématu má smysl, pokud dotaz navazuje na problém řešený v tématu - v tom případě je třeba téma odznačit, jako nevyřešené. Jinak prosím o nový dotaz do nového tématu a v přimeřené sekci fóra (takové zadání patří do SŠ), neboť:
"Čím je tvůj problém zajímavý, že jej píšeš do sekce se zajímavými úlohami." (c)
"Pokud si nejste jisti, že Váš příspěvek navazuje na diskusi v tomto tématu, založte si prosím téma vlastní." (c)
Offline
#5 08. 01. 2010 22:56
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Statistika
ad a) pokud průměrujeme geometricky součinitele (1.062,1.044,...), vyjde úrok 4.315. To mi připadá jako "férová metoda", protože pak po pěti letech dostanu to, co po průměrných pěti letech. Ale protože jsou úroky malé a exponenciální funkce v okolí jedničky skoro lineární, je celkem jedno, jestli geometricky průměrujeme součinitele nebo aritmeticky úrokové míry.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#6 08. 01. 2010 23:36 — Editoval jelena (08. 01. 2010 23:37)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Statistika
↑ Kondr:
Zdravím :-)
to co navrhuješ (součinitele) geometricky - to souhlasím - protože v takovém případě vnímam jednu hodnotu (1) jako bázovou. A je to ve výsledku stejné, jako výsledek z aritmetického průměru.
Ale samotné hodnoty úroků bych geometricky neprůměrovala (pravě proto, že tu "bázovost" nenajdu). Ještě zkusím počíst toto.
Řekla bych, že autor otázky to má v nějakém studijním materiálu hned na úvod kapitoly a ještě tučně, tak by nám mohl vnést jasno - ale s ohledem na poslední vývoj vzdělání v EU (velký nedostatek knih, jedíný příklad s překlepem a jediná účební pomůcká je Ovoce (a to ještě na plakátu) nebo vytrvalý požadavek na důkaz "nějaké" věty (snad i česky je "některé z..."), tak by příjemně překvapil.
Offline
#7 07. 10. 2010 12:09
Re: Statistika
...z daných čisel zostavte a vyplňte tabulku početnosti (x,f., relat.početnosť., relat.počet v %.
Potom vypočítajte použitím statistických vzorcov aritmet. priemer, modus, medián, rozptyl, smerodajnú odchýlku , variačné rozpätie...(úlohy majú aj svoje znaky, len ich neviem sem napísať)
35,45,55,25,65,35,65,45,65,55,65,45,55,65,45,65,55,65,55,65
..prosím vás, čo s tým mám robiť?..pomôžete?..
Offline
#8 07. 10. 2010 19:26
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Statistika
pepsikova napsal(a):
..prosím vás, čo s tým mám robiť?
Ta tabulka bude mít tři řádky, v jednom x, v druhém absolutní četnost x, ve třetím relativní četnost (tj. absolutní četnost vydělená počtem všech čísel vynásobená 100%). Přitom x nabývá hodnot od 35,45,55,65, četnost říká, kolikrát se číslo v řadě vyskytuje.
Co se týče dalších úkolů, přijde mi, že nemá cenu sem opisovat definice mediánu / modu / průměru z wikipedie ani jiných dobře zpracovaných materiálů.
Jinak prosím o dodržování pravidel fóra - zejména tu část s Vždy se snažte alespoň zběžně naznačit váš vlastní pokus a řešení předložených příkladů. Nejsme automat na řešení příkladů. a také to se zakládáním nových témat (navíc rutinní středoškolské úlohy nepatří mezi "zajímavé úlohy z pravděpodobnosti a statistiky").
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#9 02. 01. 2012 14:36
Re: Statistika
Dobrý den,
chtěl bych se zeptat jestli by si někdo věděl rady s následujícími příklady do statistiky. Nejde jen o výpočet výsledku, ale i aspoň naznačení postupu, abych si nad to potom mohl sednou a pochopit to. Děkuji
příklad 1
K dispozici je přehled počtu ujetých kilometrů vozidel v intervalech:
v intervalu od 0 do 500 km ujely celkem 3 auta,
v intervalu od 500 do 1000 km ujely celkem 3 auta,
v intervalu od 1000 do 1500 km ujely celkem 4 auta,
v intervalu od 1500 do 2000 km ujely celkem 5 auta,
Vypočítejte průměrný počet ujetých kilometrů vozidel.
Počítejte na dvě desetinná místa
interval počet aut
0-500 3
500-1000 3
1000-1500 4
1500-2000 5
příklad 2
Posuďte zisky firmy ABC za posledních 7 let pomocí
bazických a řetězových indexů
Počítejte na dvě desetinná místa
rok 2003 2004 2005 2006 2007 2008 2009
zisk 206135 230512 251870 270982 249325 216306 189997
Si
Ti
příklad 3
Tabulka obsahuje roztříděné údaje o počtu hodin absence ve firmě:
Počítejte na dvě desetinná místa
absence v hodinách (xi) 5 9 12 34 51 170
počet zaměstnanců (ni) 8 4 5 3 2 3
Vypočtěte:
střední hodnoty (modus, median), rozptyl, směrodatnou odchylku, variační koeficient,
variační rozpětí, kvartily, kvartilové rozpětí
příklad 4
Sledujte vývoj v procentech i v absolutním vyjádření na dvě desetinná místa
a) cen jednotlivých výrobků
b) tržeb za zboží A
c) celkového prodávaného množství (na úrovni běžného období)
d) souhrnně ceny výrobků ze základního i běžného období
výrobek prodej kg cena Kč/kg
základní období (q0) běžné období (q1) základní období (p0) běžné období (p1)
A 1000 1200 25 24
B 1500 1400 26 27
C 2500 2600 24 23
Offline
Téma zavřeno
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z pravděpodobnosti a statistiky
- » Statistika (TOTO TÉMA JE VYŘEŠENÉ)