Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » prubeh exponencialni funkce (TOTO TÉMA JE VYŘEŠENÉ)
#1 09. 01. 2010 21:23
prubeh exponencialni funkce
ahoj, pripravuju se na pocetni cast zkousky z matanalyzy a nemuzu nejak vyresit tenhle hlavolam, a to je prubeh funkcí f(x)=x^x a f(x)=(sin x)^cosx , u prvni funkce se totiz dela jenom prubeh pro kladna x, ale kdyz si zkusim dosadit zaporne cislo, tak to v pohode vychazi, na wolframu se zobrazuje jakasi imaginarni cast pro zaporna x, ale vubec neim co to znamena, v tom druhem pripade kdyz si to vyjadrim normalne jako exponent tak taky ztrácim cast definicniho oboru kde sinus nabyva nuly a zapornych hodnot, tenhle problem sice neni moc relevantni ve vztahu uspechu u zkousky ale neda mi to proste spat (o tom je snad ten zapal pro matematiku...)
diky za pomoc
Offline
- (téma jako vyřešené označil(a) RobbieMan)
#2 09. 01. 2010 21:47 — Editoval jelena (09. 01. 2010 21:49)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: prubeh exponencialni funkce
↑ RobbieMan:
Zdravím, dnes už bylo diskutováno. Nejlepší výklad je samozřejmě od kolegů Olina a halogana (nevšimla jsem, že bylo doplněno, omluva) děkuji autorům.
Offline
#3 09. 01. 2010 23:45
Re: prubeh exponencialni funkce
V "polovině" nul je  definován, jelikož pro
definován, jelikož pro 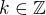 je
je  . Ale mocniny jsou ošemetné. Pokud bychom se striktně drželi definice
. Ale mocniny jsou ošemetné. Pokud bychom se striktně drželi definice  , nikdy bychom nulu neumocnili.
, nikdy bychom nulu neumocnili.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » prubeh exponencialni funkce (TOTO TÉMA JE VYŘEŠENÉ)