Matematické Fórum

Peppy · 11. 01. 2010 18:09

Ahojky ľudia trochu som sa doma nudil a tak som sa smolil v Eratosthenovom site :) a tak som si všimol zvláštnu vec: "Čísla v tvare:
$f(x) = 1.10^{2x}+1$ sú prvočísla. Odchytí to všetky čísla v takomto tvare okrem 11-tky. Čo vy na to?

Stýv · 11. 01. 2010 18:15

10001=73*137

Batrachus · 11. 01. 2010 18:43

Promiň, asi jsem blbej, ale co znamená ten vzoreček?
Když tam doplním za x prvočíslo, tak nevidím žádný rozdíl, od toho, když zadám složené číslo.
Pro
$x = 1.10^{2x}+1$ je jenom jeden výsledek.
Když hodím do WolframAlphy tvůj vzorec, tak tam nevykoukám nic, co by mohlo mít něco společného s prvočísly. Tak nevím.

Batrachus · 11. 01. 2010 18:53

Ne počkat, už jsem to pochopil. Když za x doplním množinu všech prvočísel, tak vznikne nespojitý graf tvořený body, z nichž každý se nachází v x přirozeného čísla. Zajímavý vzorec.

FailED · 11. 01. 2010 19:51 — Editoval FailED (11. 01. 2010 19:56)

↑ Peppy:
Zdravím,

tvrdíš že všechna prvočísla (kromě 11) tvaru $10^k+1, \quad k\in\mathbb{N}$ se dají napsat jako $10^{2n}+1, \quad n\in\mathbb{N}$ je to tak?

Tedy jinak řečeno neexistuje takové prvočíslo p, že $p=10^{2n+1}+1, \quad n\in\mathbb{N}$ . To je pravda.

K důkazu nám stačí znalost vzorce, nebo můžeme dokázat dělitelnost 11 podle kritéria dělitelnosti 11.
viz např. dělitelnost - ke konci jsou vypsány podmínky dělitelnosti do 20 (je tam i vysvětleno jak se takové podmínky zjistí).

↑ Batrachus: To je sarkasmus? Nebo mi něco uniká?

Batrachus · 11. 01. 2010 20:03

↑ FailED:
Ne, to není sarkasmus.

FailED · 11. 01. 2010 20:08

↑ Batrachus:

Tak asi nerozumím, funkce definovaná jen pro prvočísla určitě nebude definovaná pro jiné, než přirozené číslo.

Batrachus

↑ FailED:
Ne, měl jsem na mysli tohle:
http://www.wolframalpha.com/input/?i=Pl … rime%29%29
Každý bod se nachází nad přirozeným číslem.

FailED · 11. 01. 2010 20:26

↑ Batrachus:

To protože ty si tam tiskneš graf kde umocňuješ 1,1 na dvojnásobek x-tého prvočísla. Pořadová čísla prvočísel jsou přirozená čísla. Proto je ta funkce definovaná jen pro N.

Pavel · 12. 01. 2010 16:01 — Editoval Pavel (12. 01. 2010 16:03)

↑ Peppy:

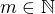Myslím si, že Tvá hypotéza je chybná. $10^{2k}+1$ není prvočíslo, pokud např. $k=3m$ , $m\in\mathbb{N}$ . Pak lze totiž toto číslo rozložit v součin:

$10^{2k}+1=10^{2\cdot 3m}+1=(10^{2m})^3+1=(10^{2m}+1)(10^{4m}-10^{2m}+1).$

Stačí využít vzorce 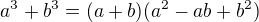$a^3+b^3=(a+b)(a^2-ab+b^2)$ .

Pak tedy např.

$m=1\qquad\Rightarrow\qquad 10^6+1=101\cdot 9901\nl m=2\qquad\Rightarrow\qquad 10^{12}+1=10001\cdot 99990001$

apod. Podobně lze dokázat, že ani v případě, kdy $k=5m$ , $k=7m$ , atd. (obecně $k=(2s+1)m$ , $s\in\mathbb{N}$ ), není $10^{2k}+1$ prvočíslo.