Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Střední škola
- » linearne nerovnice s absolutnou hodnotou (TOTO TÉMA JE VYŘEŠENÉ)
#3 10. 02. 2008 12:48 — Editoval jelena (10. 02. 2008 14:50)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: linearne nerovnice s absolutnou hodnotou
Zdravim, bude lepsi, kdyz sem napises primo tvuj priklad.
Pokud mas na mysli - jak se urcuje zavorka (otevreno - zavreno) pri uvodnim stanoveni intervalu (nulove, body, intervaly, na kterych budeme menit znamenka) - tak tam je to vcelku jedno - staci, kdyz das na konci intervalu uzavrenou, pak pro stejne cislo das na zacatku druheho intervalu otverenou.
Ale pokud mas na mysli celkove reseni, tak musi sedet ze zadanim.
Treba I x-2 I <5 nulovy bod x = 2
vytvorim intervaly pro urceni znamenka vyrazu absolutni hodnoty:
(-oo, 2), <2, +oo)
nebo
(-oo, 2>, (2, +oo) - to je uplne jedno.
Ale celkovy vysledek (-3, 7) musi mit okruhle zavorky, nebot zadani vyžaduje " mensi 5 "- interval otevreny.
Napis, prosim svuj priklad :-)
Edit: zdravim kolegu plisna :-) - opet prohravam co se tyce upravy
Offline
#4 10. 02. 2008 12:57 — Editoval plisna (10. 02. 2008 12:58)
Re: linearne nerovnice s absolutnou hodnotou
tak spocitejme treba priklad  .
.
v prvnim kroku urcime x, pro ktere nabyva argument absolutni hodnoty nulu:  .
.
nyni reseni rozdelime na dve casti, respektive budeme resit nasi nerovnici na dvou intervalech:  a
a  . predpokladam, ze te zajima, jak se urci zavorky techto intervalu. odpoved je takovato: je to na tobe, muzes je zvolit, jak chces, ale musis ten hranicni bod zahrnout ALESPON do jednoho intervalu, takze mame celkem 3 moznosti:
. predpokladam, ze te zajima, jak se urci zavorky techto intervalu. odpoved je takovato: je to na tobe, muzes je zvolit, jak chces, ale musis ten hranicni bod zahrnout ALESPON do jednoho intervalu, takze mame celkem 3 moznosti:  nebo
nebo  (tak jsem si vybral ja) a nebo jeste posledni moznost
(tak jsem si vybral ja) a nebo jeste posledni moznost  .
.
nyni resime nerovnici na intervalu  . dosadime libovolne cislo z tohoto intervalu do argumentu absolutni hodnoty, tedy do vyrazu
. dosadime libovolne cislo z tohoto intervalu do argumentu absolutni hodnoty, tedy do vyrazu  a zjistujeme, ze vyraz je ZAPORNY, tedy "otacime" znamenko v absolutni hodnote a pocitame nerovnici
a zjistujeme, ze vyraz je ZAPORNY, tedy "otacime" znamenko v absolutni hodnote a pocitame nerovnici 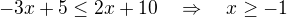 a nakonec udelame prunik s intervalem, na kterem jsme nerovnici resili:
a nakonec udelame prunik s intervalem, na kterem jsme nerovnici resili:  , tedy ziskavame prvni podvysledek
, tedy ziskavame prvni podvysledek  .
.
naprosto analogicky postupujeme u druheho intervalu, pricemz ziskame 
vysledne reseni je pak SJEDNOCENIM jednotlivych podvysledku, tedy  .
.
edit: a divam se, ze jsem byl opet pomalejsi nez jelena :) a timto ji zdravim
Offline
Stránky: 1
- Hlavní strana
- » Střední škola
- » linearne nerovnice s absolutnou hodnotou (TOTO TÉMA JE VYŘEŠENÉ)