Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Důkaz Darbouxovy věty (TOTO TÉMA JE VYŘEŠENÉ)
#1 12. 01. 2010 00:10
Důkaz Darbouxovy věty
Zdravím kolegy,
mám tady další důkaz vlastní výroby. Tentokrát asi nebude lepší, než ten z přednášky, každopádně kdyby se někomu chtělo ho omrknout, budu rád.
Znění věty:
Nechť  je spojitá na uzavřeném intervalu
je spojitá na uzavřeném intervalu ![kopírovat do textarea $[a, b]$](/mathtex/7f/7fda1308e7418bcf43f2a1f65b8f8727.gif) ,
,  . Nechť
. Nechť  a nechť
a nechť 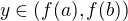 . Pak existuje bod
. Pak existuje bod  , splňující
, splňující 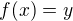 . Analogické tvrzení platí v případě, kdy
. Analogické tvrzení platí v případě, kdy  .
.
Důkaz:
Označím![kopírovat do textarea $M = \{x \in [a, b] | f(x) < y\}\nl s = \sup M$](/mathtex/e3/e3fdcfdbf9ffccd49ba12b0d7d6cde33.gif)
(množina  je neprázdná, protože obsahuje
je neprázdná, protože obsahuje  ).
).
Dokážu, že pro prvky  platí následující tvrzení:
platí následující tvrzení: .
.
To platí díky spojitosti  - vždy můžu zvolit tak malé
- vždy můžu zvolit tak malé  , že
, že 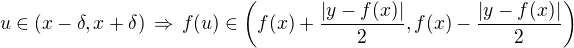 .
.
Tím pádem 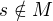 - kdyby tam totiž patřilo, muselo by tam díky výše uvedené vlastnosti být i nějaké větší číslo, což by byl spor se supremem.
- kdyby tam totiž patřilo, muselo by tam díky výše uvedené vlastnosti být i nějaké větší číslo, což by byl spor se supremem.
Nyní přidáme další písmenka:![kopírovat do textarea $N = \{x \in [s, b] | f(x) > y\}\nl t = \inf N$](/mathtex/99/99a9d262989e83b4785ff9715d4a733c.gif) .
.
(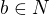 , takže
, takže  je neprázdná).
je neprázdná).
Pokud je  , jsme hotovi, protože pak
, jsme hotovi, protože pak 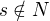 , takže neplatí ani
, takže neplatí ani  , ani
, ani  , tudíž musí platit
, tudíž musí platit 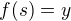 . Pokud
. Pokud 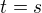 , snadno dojdeme k tomu, že
, snadno dojdeme k tomu, že 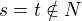 , protože množina
, protože množina  splňuje analogickou vlastnost jako
splňuje analogickou vlastnost jako  (jen v "opačném směru"), což se opět ukáže ze spojitosti. Tedy opět neplatí ani jedna z ostrých nerovností, takže
(jen v "opačném směru"), což se opět ukáže ze spojitosti. Tedy opět neplatí ani jedna z ostrých nerovností, takže 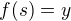 .
.
Offline
- (téma jako vyřešené označil(a) Olin)
#3 12. 01. 2010 10:23
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: Důkaz Darbouxovy věty
Hezký důkaz, jen dvě věci:
1) Když už tvrdíš  , tak by možná bylo vhodné říct, proč
, tak by možná bylo vhodné říct, proč 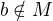 .
.
2) Možná spíš než vymýšlení nějaké konstruktu můžeš použít přímo definici spojitosti. Vím, že to je vlastně to stejné, ale mohlo by to být přehlednější: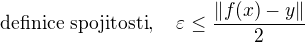
Offline
#4 12. 01. 2010 11:18
Re: Důkaz Darbouxovy věty
↑ halogan:
1) Máš pravdu. Původně jsem dokonce používal vlastnost ,
,
ale pak mi došlo, že není splněna pro  , a tak jsem použil slabší, "pravou" variantu, která však postačuje. Samozřejmě
, a tak jsem použil slabší, "pravou" variantu, která však postačuje. Samozřejmě 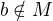 , protože
, protože  . Přišlo mi to tak zřejmé, že mě ani nenapadlo přemýšlet nad tím, že by tam
. Přišlo mi to tak zřejmé, že mě ani nenapadlo přemýšlet nad tím, že by tam  mohlo patřit.
mohlo patřit.
2) Však já jsem vlastně použil jen tu definici spojitosti. Možná to tak není přehlednější, ale přišlo mi to jako názornější, protože je "vidět", co tam ta spojitost přesně působí.
↑ RobbieMan:
Ten důkaz z přednášky se taky docela dá, vlastně využívá dost podobné věci, jako já. Jen když jsem si ho zapisoval, tak mi přišlo asi docela zřejmé, že pro 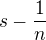 najdeme
najdeme  tak, že
tak, že 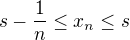 , protože to nemám v poznámkách nijak zdůvodněné. Teď už mi to tak zřejmé nepřijde, je potřeba mít nějaké znalosti o struktuře množiny
, protože to nemám v poznámkách nijak zdůvodněné. Teď už mi to tak zřejmé nepřijde, je potřeba mít nějaké znalosti o struktuře množiny  .
.
l'Hospitala dokážu, až se k němu dostanu. Pokud se mi ho podaří dokázat.
Offline
#5 12. 01. 2010 11:25
#6 12. 01. 2010 16:24
Re: Důkaz Darbouxovy věty
↑ halogan:
Jasné, díky. Pokud 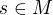 , pak je tou posloupností konstantní
, pak je tou posloupností konstantní 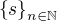 . Pokud
. Pokud 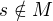 , pak pro každé
, pak pro každé 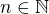 najdeme takové
najdeme takové  , že
, že 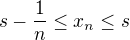 , jelikož kdybychom pro nějaké
, jelikož kdybychom pro nějaké  už takové nenašli, pak by bylo
už takové nenašli, pak by bylo 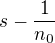 horní závorou
horní závorou  , což je spor.
, což je spor.
Offline
#7 13. 01. 2010 10:24 — Editoval Rumburak (13. 01. 2010 11:30)
Re: Důkaz Darbouxovy věty
↑ Olin:
Ahoj, připojím také několik poznámek - možná se Ti vzhledem k Tvému zájmu o analýzu budou někdy hodit.
1) Důkaz se poněkud zjednoduší po technické stránce, když od funkce f přejdeme k funkci g(x) = f(x) - y , u níž pak budeme hledat nulový bod.
2) Podstata Tvého důkazu je vyjádřena větou, která se nazývá Plíživé lemma. Na webu jsem to zatím nenašel, abych mohl dát odkaz,
ala v analýze na MFF se to, doufám, probírá.
3) Existenci nulového bodu fce g v uvažovaném intervalu I = [a, b] lze dokázat i několika dalšími způsoby, například následovně (sporem).
Abychom důkaz nekomplikovali úvahami o relativní topologii intervalu I, dodefinujme funkci g i mimo interval I:
Předpokládejme, že
(0) funkce g nemá nulový bod
a označme ![kopírovat do textarea $A \,\,:= g^{-1}[(-\infty, 0)]\,= \{\,x\in \mathbb{R}\,:\, g(x) < 0\,\}$](/mathtex/c8/c8b17f40b0add0919c1ab8fafb0574ea.gif) (tj. vzor intervalu (-oo, 0) při zobrazení g) ,
(tj. vzor intervalu (-oo, 0) při zobrazení g) , ![kopírovat do textarea $B \,\,:= g^{-1}[(0, +\infty)]\,= \{\,x\in \mathbb{R}\,:\, g(x) > 0\,\}$](/mathtex/fc/fc4692e9e0a737007f8d83f497006542.gif) (tj. vzor intervalu (0, +oo) při zobrazení g) .
(tj. vzor intervalu (0, +oo) při zobrazení g) .
Zřejmě pak (s využitím předpokladu (0))
(1) Množina  je disjunktním sjednocením množin A, B .
je disjunktním sjednocením množin A, B .
Dále: Každá z množin A, B je otevřená (neboť je vzorem otevřené množiny při spojitém zobrazení).
Z tohoto a z (1) plyne, že A, B jsou obojetnými množinami v  (obojetná mn. je taková, která je zároveň otevřená i uzavřená).
(obojetná mn. je taková, která je zároveň otevřená i uzavřená).
Jedinými obojetnými množinami v  jsou, jak známo,
jsou, jak známo,  a prázdná množina. Z toho již snadno odvodíme spor.
a prázdná množina. Z toho již snadno odvodíme spor.
Offline
#8 13. 01. 2010 15:01
Re: Důkaz Darbouxovy věty
↑ Rumburak:
Díky, zajímavý důkaz. Ve svých důkazech se snažím obvykle vyhnout použití otevřených a uzavřených množin, protože ačkoliv tyto pojmy znám, na přednášce jsme si je nedefinovali.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Důkaz Darbouxovy věty (TOTO TÉMA JE VYŘEŠENÉ)