Matematické Fórum

Petuhik · 04. 01. 2010 10:57

Ahoj potřebovala bych poradit s několika příklady ohledně nekonečných řad. Prosím, pomožte mi :-(

- příklad: Napsat číslo e^-8 jako soušet nekonečné číselné řady.

Olin · 04. 01. 2010 12:14

$\mathrm{e}^x = \exp(x) = \sum_{n=0}^{\infty} \frac{x^n}{n!}$

Dosaď za $x$ .

Rumburak

Vyjdeme z Maclaurinova rozvoje exponenciální funkce
$\text{e}^{\,x} \,\,=\,\, \sum_{n=0}^{\infty}\,\frac{x^n}{n \,!}$ ,

kam dosadíme $x = -8$ a upravíme:
$\text{e}^{\,-8} \,\,=\,\, \sum_{n=0}^{\infty}\,\frac{(-8)^n}{n \,!} \,\,=\,\, \sum_{n=0}^{\infty}\,\frac{(-1)^n 2^{3n}}{n \,!}$

PS. Kolega byl rychlejší, ale už to tu nechám.

Petuhik · 04. 01. 2010 12:34

↑ Rumburak:

ahaaa. A to je tedy celý příklad??Děkuji moc:-)

Petuhik · 04. 01. 2010 12:38

2. určení Taylorového rozvoje funkce arctan x, z toho obor konvergence této řady a vyjádření čísla pí jako součet nekonečné číselné řady.

Rumburak

↑ Petuhik:
Pro $x \in (-1, \,1)$ je $\frac {1}{1 + x^2} = \sum_{n=0}^\infty (-x^2)^n = \sum_{n=0}^\infty (-1)^n x^{2n}$ (geom. řada s kvocientem $-x^2$ ).
Integrací poslední identity dostáváme

(1) $\text{arctg} x \,+ C= \sum_{n=0}^\infty \frac {(-1)^n}{2n + 1}\, x^{2n + 1}$ ,
Dosazaním $x=0$ spočítáme hodnotu integrační konstanty $C = 0$ .
Z Leibnizova ktiteria plyne, že řada v (1) konverguje též pro 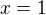$x = 1$ a $x = -1$ , tj. obor její konvergence (v reálném oboru)
je uzavřený interval $[-1, \,1]$ .
Abelova věta pro mocninné řady pak dává
$\text{arctg}\, 1 = \sum_{n=0}^\infty \frac {(-1)^n}{2n + 1}\, 1^{2n + 1} = \sum_{n=0}^\infty \frac {(-1)^n}{2n + 1}$ ,
kde, jak víme, $\text{arctg}\, 1 = \frac{1}{4}\pi$ .

Petuhik · 04. 01. 2010 14:32

↑ Rumburak:

Děkuji moc. Ty seš opravdu machr. Klobouk dolů. Mochla bych otravovat ještě s pár příkladama? Já bych s tím opravdu nepohla :-(a docela ti závidím že ti to tak jde.

úkol je: určit obor konvergence a rozhodnout, kdy je řada konverguje stejnoměrně.

1.suma {n=1} {oo} 11/n^x
2.suma {n=1} {oo} n^12/x^n
3.suma {n=1} {oo} ln (1+(x^13/n*ln^(2)(n))
4.suma {n=1} {oo} 14x/(x^(2)+n^(7))

Rumburak · 04. 01. 2010 14:40

↑ Petuhik:
Uznání potěší :-) Mohu se kouknout i na další úlohy, ale dnes už se k tomu nedostanu, třeba mezitím pomůže i někdo další.

Petuhik

↑ Rumburak:

je to pravda, tak ti to prostě musím napsat. Vážně tě obdivuji. A budu moc ráda, když by ses pak ještě koukl na tento příklad:
Vyjádřit funkci sin x / x jako součet mocninné řady, u této řady určit ještě poloměr konvergence a vypočítat

2
∫ (sinx / x) dx s přesností na 3 desetinná místa.
1

A vážně si toho moc vážím. Děkuju

Rumburak

úkol je: určit obor konvergence a rozhodnout, kdy je řada konverguje stejnoměrně.

(1) suma {n=1} {oo} 11/n^x

Zde činitel 11 není důležitý, x je parametr. Konvergenci řeší integrální kriterium - řada je konvergentní, pokud x > 1.
Konvergence NENÍ stejnoměrná na celém (1, oo), protože v bodě 1 (zprava) to "uteče" (viz Riemannova Zeta funkce).
Konvergence však JE stejnoměrná na každém intervalu [t, oo) , kde t > 1 , protože pak řada suma {n=1} {oo} 11/n^t
je společnou konvergentní majorantní řadou pro všechny řady (1), v nichž x in [t, oo) . Jde tedy o konvergenci lokálně stejnoměrnou
v (1, oo).

(2) suma {n=1} {oo} n^12/x^n

D'Alembertovo kriterium dává konvergnci pro |x| > 1 . Pro x = 1 resp. x = -1 nastane divergence , neboť pak neplatí, že posloupnost
tvořící řadu má limitu rovnu 0, což je nutná podmínka pro konvergenci řady.
Obdobným způsobem jako v úloze 1 se využije skutečnost, že pro t > 1 je řada suma {n=1} {oo} n^12/t^n konvergentní majorantní řadou
pro všechny řady (2), v nichž |x| >= t . Jde tedy opět o lokálně stejnoměrnou konvergenci řady (2) pro |x| > 1. Konvergence však v celém
tomto rozsahu stejnoměrná není, protože v blízkosti bodů x = 1 , x = -1 to opět "utíká".

(3) suma {n=1} {oo} ln (1+(x^13/n*ln^(2)(n))
Nejsem si jist, zda jsem to správně rozluštil - zkus to lépe uzávorkovat nebo jinak to zpřehlednit .

(4) suma {n=1} {oo} 14x/(x^(2)+n^(7))

Označme $f_n(x) \,\,:= \frac {14x}{x^2 + n^7}$ . Vyšetřením průběhu této funkce zjistíme, že nabývá svého absolutního minima v bodě $x_1 = -n^{\frac{7}{2}}$
a absolutního maxima v bodě $x_2 = n^{\frac{7}{2}}$ . Funkce tato je lichá, proto
$M_n \,\,:=\,\,\sup_{x \in (-\infty, \infty)} |f_n(x)| = f_n(x_2) = \frac {14n^{\frac{7}{2}}}{2n^7}= 7n^{-\frac{7}{2}}$ .

Řada sestavená z členů M_n je konvergentní podle integrálnáho kriteria (viz též úloha 1) , našli jsme tak konvergentní majorantní řadu k řadě (4)
na celé reálné ose. Řada (4) proto konverguje na celé reálné ose, a to stejmoměrně (tamtéž).

Rumburak

↑ Petuhik:
Zde jsou příklady nejdůležitějších T. rozvojů:
http://cs.wikipedia.org/wiki/Taylorova_ … va_rozvoje

Z rozvoje pro sin x snadno najdeme rozvoj pro (sin x) / x (tím, že každý člen řady pro sin x vydělíme číslem x).
Obě řady konvergují lokálně stejnoměrně uvnitř kruhu s týmž poloměrem konvergence +oo, což se dá ověřit pomocí
d'Alembertova kriteria s použitím obecné věty o chování mocninné řady uvnitř konv. kruhu.
Při integraci takovéto funkční řady přes omezený uzavřený interval ležící uvnitř konv. kruhu lze vzájemně zaměnit pořadí sumy
a integrálu, což nutno provést. Zkus to sama, jistě to zvládneš, a až budeš mít výsledek ve tvaru řady (už nezávislé na x, protože
dle x se prováděl určitý integrál), pošli to sem a můžeme zkusit probrat tu "přesnost".

Petuhik · 09. 01. 2010 12:44

↑ Rumburak:

myslím, že správný zápis u toho oboru konvergnce příklad č. 3 je:

suma {n=1} {oo} ln [{1+(x^13/n*(ln^(2))*(n))}]

děkuji

Petuhik · 09. 01. 2010 12:46

↑ Rumburak:

Zkoušela jsem podle toho tvého návodu ten úkol s tím sin/x.

1. se měla tato funkce vyjádřit jako součet mocnniné řady.
To mi vyšlo toto:
sinx/x = 1 - (x^2)/3! + (x^4)/5! - (x^6)/7! + ........((-1)^n)*(x^(2n))/(2n+1)! + .....

Ohledně té integrace jsem došla na toto, a dále nevím jak pokračovat aby to bylo vypočítané s přesností na tři desetinná místa.

2 2
∫ (sinx/x)dx = [x - ((x^3)/3*3!)+ ((x^5)/5*5!) - ((x^7)/7*7!) + ....+ ((-1)^n)*(x^(2n+1))/(2n+1)*(2n+1)! +....]
1 1

Opět děkuji za pomoc.

Rumburak

↑ Petuhik:
Správně. Máme tedy vyjádřeno řadou

$S\,\,:=\int_1^2\frac{\sin\,x}{x}\text{d} x = \sum_{n=0}^\infty \[(-1)^n \frac{x^{2n+1}}{(2n+1)\cdot (2n+1)!}\]_{x=1}^2 =\sum_{n=0}^\infty (-1)^n \frac{2^{2n+1} \,-\, 1}{(2n+1)\cdot (2n+1)!}$ .

Označme $a_n \,:= \frac{2^{2n+1} \,-\, 1}{(2n+1)\cdot (2n+1)!}$ . Zřejmě jde o posloupnost kladných čísel, jejíž limita je 0.
Pokud by se podařilo dokázat, že je nerostoucí, pak podle Leibnizovy věty by bylo

(X) $\|S\,-\,\sum_{n=0}^k (-1)^n \frac{2^{2n+1} \,-\, 1}{(2n+1)\cdot (2n+1)!}\| = \|S\,-\,\sum_{n=0}^k (-1)^n a_n\| \,\le \,a_{k+1}$ .

Je možné, že nerostoucí monotonie té posloupnosti funguje až od určitého indexu výše, pak by se to promítlo do rozsahu platnosti odhadu (X).
Tohoto odhadu využijeme:
Stačí nalézt nejmenší přirozené číslo k, pro které $a_{k+1}\, <\, 10^{-3}$ .

Bohužel nemám teď moc času věnovat se tomu podrobněji.
Příležitostně ještě zapřemýšlím o té zbývající úloze, ale pokud na to spěcháš, tak to radši zkus zároveň sama, je možné, že budeš rychlejší.

PS.
Poloměr konvergence řady z rozvoje
$\int_0^z\frac{\sin\,x}{x}\text{d} x = \sum_{n=0}^\infty (-1)^n \frac{z^{2n+1}}{(2n+1)\cdot (2n+1)!}$
je týž jako u Maclaurinova rozvoje funkce sin , tedy +oo .

Rumburak

↑ Petuhik:
Z toho zápisu

(A) suma {n=1} {oo} ln [{1+(x^13/n*(ln^(2))*(n))}]

nejsem o mnoho chytřejší. Zkusme výraz (A) postupně zanalyzovat. Nejprve to trochu zpřehledníme vložením mezer:

(B) suma {n=1} {oo} ln [{ 1 + (x^13/n*(ln^(2))*(n)) }] ,

vidíme, že hranaté závorky [ ... ] jsou nadbytečné - postačí ty složené { ... }, máme tedy

(C) suma {n=1} {oo} ln { 1 + (x^13/n*(ln^(2))*(n)) } .

Nyní se podívejme na člen

(D) y = (x^13/n*(ln^(2))*(n))

z té složené závorky. V něm se rovněž vyskytují některé závorky nabytečně, např. ve výrazech (2) , (n) . Po jejich odstranění máme

(E) y = (x^13/n*(ln^2)*n) .

Nadbytečné jsou i vnější závorky, takže místo rovnosti (E) můžeme směle psát

(F) y = x^13/n*(ln^2)*n .

Nyní se ale objevují problémy ve výkladu této syntaxe:
1. Co je to (ln^2)*n (neboli logaritnus na druhou KRÁTE n ) ?
2. Co všechno patří do jmenovatele zlomku ?
3. Je v čitateli zlomku jen ta 13 nebo celé x^13 ?
4. Co všechno patří do exponentu u x ?

Pokud jsem navrhoval lepší uzávorkování, tak jsem měl na mysli otázky 2, 3, 4 - zde by závorky zbytečné nebyly.

Matematické Fórum

#1 04. 01. 2010 10:57

matematická analýza

#2 04. 01. 2010 12:14

Re: matematická analýza

#3 04. 01. 2010 12:20 — Editoval Rumburak (04. 01. 2010 12:27)

Re: matematická analýza

#4 04. 01. 2010 12:34

Re: matematická analýza

#5 04. 01. 2010 12:38

Re: matematická analýza

#6 04. 01. 2010 14:07 — Editoval Rumburak (04. 01. 2010 14:12)

Re: matematická analýza

#7 04. 01. 2010 14:32

Re: matematická analýza

#8 04. 01. 2010 14:40

Re: matematická analýza

#9 04. 01. 2010 15:57 — Editoval Petuhik (04. 01. 2010 16:54)

Re: matematická analýza

#10 05. 01. 2010 09:49 — Editoval Rumburak (05. 01. 2010 15:19)

Re: matematická analýza

#11 05. 01. 2010 14:32 — Editoval Rumburak (05. 01. 2010 15:04)

Re: matematická analýza

#12 09. 01. 2010 12:44

Re: matematická analýza

#13 09. 01. 2010 12:46

Re: matematická analýza

#14 11. 01. 2010 11:53 — Editoval Rumburak (11. 01. 2010 13:56)

Re: matematická analýza

#15 14. 01. 2010 10:34 — Editoval Rumburak (14. 01. 2010 12:06)

Re: matematická analýza

Zápatí