Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » Lednová limita (TOTO TÉMA JE VYŘEŠENÉ)
#2 15. 01. 2010 13:39 — Editoval Rumburak (15. 01. 2010 13:40)
Re: Lednová limita
Offline
#3 15. 01. 2010 14:39
#4 15. 01. 2010 14:59
#5 15. 01. 2010 21:42
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Lednová limita
Hezké. Bohužel (nebo bohudík?) jsem omylem (chyba ve výpočtu) vyřešil jiné zadání, tak se o něj podělím. Možná půjde vyřešit nějakou modifikací Rumburakova postupu, já jsem ho ale řešil jinak.
Offline
#6 15. 01. 2010 22:25 — Editoval Pavel (15. 01. 2010 22:27)
Re: Lednová limita
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#7 15. 01. 2010 22:32
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Lednová limita
↑ Pavel:
Přesně tak jsem to řešil a došel jsem ke stejnému výsledku :-).
Offline
#8 15. 01. 2010 22:34
Re: Lednová limita
↑ BrozekP:
Zkoušel jsem právě takto řešit i původní limitu, bohužel nepodařilo se mi z ní vhodně vytknout.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » Lednová limita (TOTO TÉMA JE VYŘEŠENÉ)

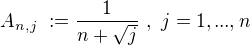 a odhadujme :
a odhadujme :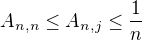 ,
, ,
,  , což má limitu 1 , takže
, což má limitu 1 , takže ¨.
¨.![kopírovat do textarea $[0,1]$](/mathtex/52/520897da7413e2014a7783a154b21dba.gif) na
na  stejných částí, kde
stejných částí, kde 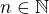 . Pak
. Pak 
 při tomto ekvidistantní dělení intervalu
při tomto ekvidistantní dělení intervalu 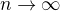 přejde tento dolní součet v určitý integrál
přejde tento dolní součet v určitý integrál