Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 16. 01. 2010 13:04
Lineární nerovnice
Dobrý den, potřebovala bych od vás zkontrolovat následující nerovnici:
(5-x) / (x-1) + (1+4x) / (2x+2) < 1
(2x+2) * (5-x) + (x-1) * (1+4x) < 2* (x+1)*(x-1)
2x^2 + 5x + 9 < 2x^2 - 2
5x < -11
x < -11/5
a podmínky: X se nesmí rovnat +1; x se nesmí rovnat - 1
Děkuji moc
Offline
- (téma jako vyřešené označil(a) Hanys113)
#2 16. 01. 2010 13:09
Re: Lineární nerovnice
↑ Hanys113:
není to dobře. V nerovnicích s neznámou ve jmenovateli nelze takto odstraňovat zlomky.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#4 16. 01. 2010 13:18
Re: Lineární nerovnice
↑ Hanys113:
převeď 1 na levou stranu, uprav výraz, rozlož v součin a řeš nerovnici metodou nulových bodů.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#7 16. 01. 2010 14:12 — Editoval gladiator01 (16. 01. 2010 14:16)
- gladiator01


- Místo: Jindřichův Hradec
- Příspěvky: 1587
- Škola: ZČU FAV - SWI
- Pozice: absolvent
- Reputace: 53
- Web
Re: Lineární nerovnice
↑ Hanys113:
Máš to dobře, teď stanov nulové body
Naděje jako svíce jas, potěší srdce štvané, čím temnější je noční čas, tím zářivěji plane.
VIVERE - MILITARE EST (Seneca)
Vím, že nic nevím. - Sokrates
Offline
#16 16. 01. 2010 15:22 — Editoval Reshi (16. 01. 2010 15:25)
Re: Lineární nerovnice
no ja by som odporucal si to hodit do tabulky kde hore zlava do prava budes mat jednotlive intervaly ako (-nekonecno,-11/5), <-11/5,-1) atd a pod sebou v tabulke budes mat 5x+11 potom 2(x-1) potom x+1 a potom si tam daj kolonku ze spolu .... dosadzaj posupne cisla z intervalov do jednotlivych vyrazov (napr -2 si dosadis do 5x+11 teda vznikne 5*(-2)+11) a prejednotlive tieto ciastkove vyrazy ti vychadzaju kladne a zaporne cisla (do koloniek si nezapisuj cel eciasla ale len znamienka vysledko ci je kladny alebo zaporny) . Tie potom v stlpci pod sebou prenasobis (prenasobis znamienka to znamena ze ked mas napr +*+*- = - , do spolu zapises minus, potom napr -*-*+ = + do spolu napsies plus.)takto budes mat ostavenu tabulku a v nej popisane pre kazdy interval ci je celkovo (spolu) kladny alebo zaporny. To spolu vyjadruje aky bude zlomok ci bude mat pred sebou znamienko + teda bude vacsi ako 0 alebo tam bude mat - a bude mensi ako nula. Teraz sa pozri ktore intervaly v tvojom pripade su zaporne (tie su u teba riesenim) a vypis ich ako korene. (pokial by mal aj znamienko rovna sa vacsi alebo rovnasa mensi tak tam patri aj nulovy bod do intervalu riesenia ).
Offline

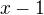 ,
, 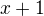 a
a 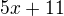 ) měnit svá znaménka.
) měnit svá znaménka.