Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 16. 01. 2010 10:18
Re: limita fcie
↑ jarrro:
Prosímtě, ten poslední krok jsi provedl jak? Přijde mi to jako nějaké použití l'Hospitala, přitom ten vede na mnohem jednodušší limitu
Standartní postupy jako rozšíření  mě taky na tvůj upravený tvar nějak nevedou. S konečným výsledkem ale souhlasím.
mě taky na tvůj upravený tvar nějak nevedou. S konečným výsledkem ale souhlasím.
Offline
#5 16. 01. 2010 13:01
Re: limita fcie
OK diky moc ludia, uz som na to prisiel neskor aj ja ako na to, cez pouzitie ecka a potom ln(1+x)/x ale aj tak diky.
A mal by som tu este jednu kde mi to za pomoci toho isteho principu nejde a lamem si s tym hlavu, hlavne chcem to riesit bez LH:
lim x k +nekonecnu (ln(x^2-x+1))/(ln(x^10+x+1))
Vopred diky
Offline
#17 16. 01. 2010 20:14
Re: limita fcie
Ono to bude asi jedno, jaký to je. Každopádně každý logaritmus umíme převést na přirozený vztahem  . Dosazením
. Dosazením  obdržíme rovnost
obdržíme rovnost  , pomocí které již dostaneme požadovaný výsledek.
, pomocí které již dostaneme požadovaný výsledek.
Offline

 limita exponentu je
limita exponentu je pôvodná limita je jedna
pôvodná limita je jedna cize
cize  potom vyjmul logaritmy podla sucinu logaritmov na
potom vyjmul logaritmy podla sucinu logaritmov na  a dalej tym vydelnim
a dalej tym vydelnim  sa to akoze ulahci? malo by to vyjst 1/5 ale z tych polynomov co mi tu vychadzaju to je 0. tak neviem vazne
sa to akoze ulahci? malo by to vyjst 1/5 ale z tych polynomov co mi tu vychadzaju to je 0. tak neviem vazne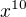 , jak doporučil kolega v závorce.
, jak doporučil kolega v závorce.

 , protože to nám jde do nuly a dá se přes aritmetiku odstranit. Proto to vytýkání.
, protože to nám jde do nuly a dá se přes aritmetiku odstranit. Proto to vytýkání.


 .
. ale mne vyslo
ale mne vyslo  a
a 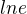 je jedna nie
je jedna nie  tak som si neni tym isty
tak som si neni tym isty čo je minus derivácia funkcie
čo je minus derivácia funkcie  v bode z=x^2
v bode z=x^2