Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » Poskakování na číselné ose (TOTO TÉMA JE VYŘEŠENÉ)
#1 16. 01. 2010 18:46 — Editoval Marian (16. 01. 2010 20:15)
Poskakování na číselné ose
Jedna z dalších velmi snadných úloh ...
Nechť jsou dána dvě reálná čísla  a
a  . Definujme posloupnost
. Definujme posloupnost  , kde
, kde  ,
,  . Najděte limitu
. Najděte limitu 
_____________
Při řešení nepoužívejte techniku diferenčních rovnic. Použijte aparát SŠ; máte-li chuť, nadpis může usnadnit úvahu. Ovšem řešení chci absolutně korektní.
Offline
- (téma jako vyřešené označil(a) Marian)
#2 16. 01. 2010 20:07 — Editoval Pavel (16. 01. 2010 20:08)
Re: Poskakování na číselné ose
Až pozdě jsem si přečetl, že technika diferenčních rovnic je zapovězena :-)
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#4 16. 01. 2010 20:19 — Editoval Pavel (16. 01. 2010 23:09)
Re: Poskakování na číselné ose
Nevím, zda je toto řešení jednodušší než mé předchozí, avšak vystačím si zde pouze ze SŠ znalostmi - matematická indukce, nekonečná geom. řada a základy teorie posloupností.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#5 16. 01. 2010 21:35 — Editoval lukaszh (16. 01. 2010 21:35)
Re: Poskakování na číselné ose
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
#6 16. 01. 2010 22:21
#7 17. 01. 2010 08:23
Re: Poskakování na číselné ose
↑ Pavel:↑ lukaszh:↑ Kondr:
Pavlovo řešení je skutečně kompletní, idea u lukaszhe je stejná jako u Pavla. To, co však předvádí Kondr, je velmi zajímavé. K takovému řešení jsem nedospěl, ale přemítal jsem podobné myšlenky.
Pochvala všem ...
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » Poskakování na číselné ose (TOTO TÉMA JE VYŘEŠENÉ)

 v explicitním tvaru. Tj
v explicitním tvaru. Tj
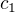 a
a  jsou reálné konstanty. Ty určíme z počtátečních podmínek. Takže
jsou reálné konstanty. Ty určíme z počtátečních podmínek. Takže
 k nekonečnu:
k nekonečnu:
 pomocí prvních dvou
pomocí prvních dvou 

 . První indukční předpoklad je očividně splněn. Předpokládejme dále, že obě identity platí až po jisté
. První indukční předpoklad je očividně splněn. Předpokládejme dále, že obě identity platí až po jisté 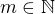 . Dokažme, že tyto platí i pro
. Dokažme, že tyto platí i pro  .
.  ,
, 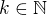 . Pak
. Pak ![kopírovat do textarea $ \begin{align*} \frac 12\,(x_m+x_{m-1})&=\frac 12\,(x_{2k}+x_{2k-1})=\frac 12\biggl[\frac 12\,x_1\sum_{i=0}^{k-1}\frac 1{4^i}\,+\,\frac 14\,x_0\biggl(\sum_{i=0}^{k-2}\frac 1{4^i}\,+\,\frac 1{2\cdot 4^{k-2}}\biggr)\,+\,\frac 12\,x_1\biggl(\sum_{i=0}^{k-2}\frac 1{4^i}\,+\,\frac 1{2\cdot 4^{k-2}}\biggr)\,+\,\frac 14\,x_0\sum_{i=0}^{k-2}\frac 1{4^i}\biggr]=\nl &=\frac 12\biggl[\frac 12\,x_1\biggl(\sum_{i=0}^{k-1}\frac 1{4^i}\,+\,\sum_{i=0}^{k-2}\frac 1{4^i}\,+\,\frac 1{2\cdot 4^{k-2}}\biggr)\,+\,\frac 14\,x_0\biggl(\sum_{i=0}^{k-2}\frac 1{4^i}\,+\,\frac 1{2\cdot 4^{k-2}}\,+\,\sum_{i=0}^{k-2}\frac 1{4^i}\biggr)\biggr]=\nl &=\frac 12\biggl[\frac 12\,x_1\biggl(\,2\sum_{i=0}^{k-2}\frac 1{4^i}\,+\,\frac 1{4^{k-1}}\,+\,\frac 1{2\cdot 4^{k-2}}\biggr)\,+\,\frac 14\,x_0\biggl(\,2\sum_{i=0}^{k-2}\frac 1{4^i}\,+\,\frac 1{2\cdot 4^{k-2}}\biggr)\biggr]=\frac 12\,x_1\biggl(\sum_{i=0}^{k-2}\frac 1{4^i}\,+\,\frac 1{2\cdot 4^{k-1}}\,+\,\frac 1{4^{k-1}}\biggr)\,+\,\frac 14\,x_0\biggl(\sum_{i=0}^{k-2}\frac 1{4^i}\,+\,\frac 1{4^{k-1}}\biggr)=\nl &=\frac 12\,x_1\biggl(\sum_{i=0}^{k-1}\frac 1{4^i}\,+\,\frac 1{2\cdot 4^{k-1}}\biggr)\,+\,\frac 14\,x_0\sum_{i=0}^{k-1}\frac 1{4^i}=x_{2k+1}=x_{m+1}. \end{align*} $](/mathtex/9d/9dc7660808dc2989ce58a040df1ba9b4.gif)
 ,
, ![kopírovat do textarea $ \begin{align*} \frac 12\,(x_m+x_{m-1})&=\frac 12\,(x_{2k-1}+x_{2k-2})=\frac 12\biggl[\frac 12\,x_1\biggl(\sum_{i=0}^{k-2}\frac 1{4^i}\,+\,\frac 1{2\cdot 4^{k-2}}\biggr)\,+\,\frac 14\,x_0\sum_{i=0}^{k-2}\frac 1{4^i}\,+\,\frac 12\,x_1\sum_{i=0}^{k-2}\frac 1{4^i}\,+\,\frac 14\,x_0\biggl(\sum_{i=0}^{k-3}\frac 1{4^i}\,+\,\frac 1{2\cdot 4^{k-3}}\biggr)\biggr]=\nl &=\frac 12\biggl[\frac 12\,x_1\biggl(\sum_{i=0}^{k-2}\frac 1{4^i}\,+\,\frac 1{2\cdot 4^{k-2}}\,+\,\sum_{i=0}^{k-2}\frac 1{4^i}\biggr)\,+\,\frac 14\,x_0\biggl(\sum_{i=0}^{k-2}\frac 1{4^i}\,+\,\sum_{i=0}^{k-3}\frac 1{4^i}\,+\,\frac 1{2\cdot 4^{k-3}}\biggr)\biggr]=\nl &=\frac 12\biggl[\frac 12\,x_1\biggl(\,2\sum_{i=0}^{k-2}\frac 1{4^i}\,+\,\frac 1{2\cdot 4^{k-2}}\biggr)\,+\,\frac 14\,x_0\biggl(\,2\sum_{i=0}^{k-3}\frac 1{4^i}\,+\,\frac 1{4^{k-2}}\,+\,\frac 1{2\cdot 4^{k-3}}\biggr)\biggr]=\frac 12\,x_1\biggl(\sum_{i=0}^{k-2}\frac 1{4^i}\,+\,\frac 1{4^{k-1}}\biggr)\,+\,\frac 14\,x_0\biggl(\sum_{i=0}^{k-3}\frac 1{4^i}\,+\,\frac 1{2\cdot 4^{k-2}}\,+\,\frac 1{4^{k-2}}\biggr)\biggr]=\nl &=\frac 12\,x_1\sum_{i=0}^{k-1}\frac 1{4^i}\,+\,\frac 14\,x_0\biggl(\sum_{i=0}^{k-2}\frac 1{4^i}\,+\,\frac 1{2\cdot 4^{k-2}}\biggr)=x_{2k}=x_{m+1}. \end{align*} $](/mathtex/60/6053c42fe1291a2259cb6f0d503ff40b.gif)
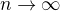 dostáváme, že
dostáváme, že

 a tento bod leží presne v strede intervalu. Teda
a tento bod leží presne v strede intervalu. Teda 
 .
. 

 a jsme v úplném metrickém prostoru. Označme L(a,b) hodnotu hledané limity pro x_0=a, x_1=b.
a jsme v úplném metrickém prostoru. Označme L(a,b) hodnotu hledané limity pro x_0=a, x_1=b.