Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 17. 01. 2010 09:44 — Editoval renewal (17. 01. 2010 10:05)
Goniometrické funkcie
Zdravím, potreboval by som pomôcť s týmto príkladom (je tam aj môj postup riešenia ktorý k ničomu neviedol):
a ešte by som sa chcel opýtať či je toto správne, či to nemá byť sin^2 alfa -cos^2 alfa (nechcel som kvôli tomu zakladať novú tému)
Ďakujem za odpoveď.
Offline
- (téma jako vyřešené označil(a) renewal)
#4 17. 01. 2010 10:11
Re: Goniometrické funkcie
Jedna krát jedna je " tisíckrát " jedna :-)
Offline
#9 17. 01. 2010 11:04
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Goniometrické funkcie
↑ renewal: může být? Zdravím.
Offline
#10 17. 01. 2010 11:15 — Editoval Ivana (17. 01. 2010 11:20)
Re: Goniometrické funkcie
↑ renewal:
pokud jsem neudělala chybu vyšlo mi :
Jedna krát jedna je " tisíckrát " jedna :-)
Offline
#12 17. 01. 2010 11:24 — Editoval Ivana (17. 01. 2010 11:24)
Re: Goniometrické funkcie
↑ renewal: už to jsem to opravila vyšlo :  :-)
:-)
Jedna krát jedna je " tisíckrát " jedna :-)
Offline
#14 17. 01. 2010 11:29
Re: Goniometrické funkcie
↑ renewal:... jdi výraz po výrazu a sleduj postup , jsou to jen jednoduché vzorce a pamatuj ... mocnitelé se při násobení sčítají
máš chybu ve vyjádření některých výrazů .....
platí ...  a
a 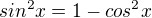
Jedna krát jedna je " tisíckrát " jedna :-)
Offline

 , v tomto pořadí.
, v tomto pořadí.
.jpg)
 . Myslím, že tohle se po tobě chtělo.
. Myslím, že tohle se po tobě chtělo. (samozřejmě podmínky)
(samozřejmě podmínky)